3. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
3.1. Диэлектрики. Полярные и неполярные молекулы
К диэлектрикам относят вещества, практически не проводящие электрического тока. Это значит, что в диэлектриках в отличие, например, от проводников нет зарядов, способных перемещаться на значительные (в сравнении с размерами самих молекул) расстояния, создавая ток. Диэлектрики состоят либо из нейтральных молекул, либо из ионов, находящихся в узлах кристаллической решетки (например, NaCl). Сами молекулы могут быть полярными и неполярными.
Положительный заряд молекулы равен суммарному заряду ядер и помещается в «центре тяжести» положительных зарядов; отрицательный заряд равен суммарному заряду электронов и помещается в «центре тяжести» отрицательных зарядов.
Для симметричных молекул (молекулы кислорода О2, водорода Н2, гелия Не и т.д.) в отсутствие электрического поля центры положительных и отрицательных зарядов совпадают, поэтому собственный дипольный момент молекулы 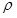 равен нулю. Такие молекулы называются неполярными (рис.3.1,а). При внесении такой молекулы во внешнее электрическое поле индуцируется дипольный момент равен нулю. Такие молекулы называются неполярными (рис.3.1,а). При внесении такой молекулы во внешнее электрическое поле индуцируется дипольный момент 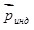 (рис.3.1,б). (рис.3.1,б).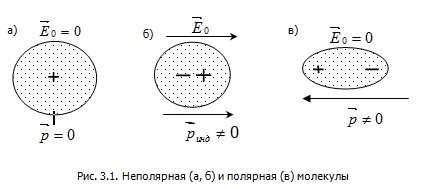
У несимметричных молекул (таких как вода H2O, соляная кислота, аммиак и т.д.) в отсутствие электрического поля центры положительных и отрицательных зарядов не совпадают, такие молекулы обладают собственным дипольным моментом 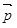 и называются полярными. и называются полярными.
3.2. Характеристики, вводимые для описания
электрического поля в присутствии диэлектриков
- Поляризация. Под действием внешнего электрического поля происходит поляризация диэлектрика. Независимо от строения диэлектрика в процессе поляризации все положительные заряды смещаются по полю, а отрицательные против поля. Как правило, смещения зарядов малы даже по сравнению с размерами молекул, это связано с тем, что напряженность внешнего поля, действующего на диэлектрик, значительно меньше напряженности внутренних электрических полей в молекулах.
- Связанные и сторонние заряды. При наличии внешнего электростатического поля на поверхности диэлектрика появляются нескомпенсированные заряды. Они находятся внутри молекул и не могут свободно перемещаться внутри диэлектрика, поэтому их называют связанными.
Заряды, которые не входят в состав молекул диэлектрика, называют сторонними. Эти заряды могут находиться как внутри, так и вне диэлектрика.
- Поле в диэлектрике. Полем
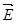 внутри диэлектрика будем называть величину, являющуюся суперпозицией поля внутри диэлектрика будем называть величину, являющуюся суперпозицией поля 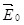 сторонних зарядов и поля сторонних зарядов и поля 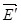 связанных зарядов: связанных зарядов:
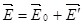 . (3.1) . (3.1)
- Диэлектрическая проницаемость среды E показывает, во сколько раз модуль напряженности
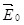 поля в вакууме больше модуля напряженности поля в вакууме больше модуля напряженности 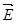 поля внутри диэлектрика: поля внутри диэлектрика:
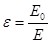 . (3.2) . (3.2)
Формула (3.2) справедлива для однородного изотропного диэлектрика.
Когда между векторами 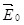 и и 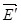 угол равен 1800, выражение (3.1) примет вид: угол равен 1800, выражение (3.1) примет вид:
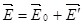 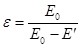 . (3.3) . (3.3)
В зависимости от формы диэлектрика и его расположения во внешнем электрическом поле угол между векторами 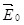 и и 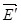 может изменяться, но всегда внутри диэлектрика электрическое поле связанных зарядов ослабляет внешнее электрическое поле (Е<E0). может изменяться, но всегда внутри диэлектрика электрическое поле связанных зарядов ослабляет внешнее электрическое поле (Е<E0).
- Поляризованность диэлектрика
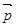 равна векторной сумме дипольных моментов молекул, находящихся в единице объема диэлектрика: равна векторной сумме дипольных моментов молекул, находящихся в единице объема диэлектрика:
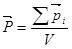 . (3.4) . (3.4)
Поляризованность 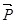 описывает способность диэлектрика создавать свое собственное поле описывает способность диэлектрика создавать свое собственное поле 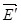 . Можно показать, что . Можно показать, что
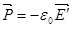 . (3.5) . (3.5)
Опытным путем была установлена формула
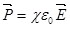 , (3.6) , (3.6)
где 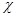 – диэлектрическая восприимчивость диэлектрика; ε0 – электрическая постоянная. – диэлектрическая восприимчивость диэлектрика; ε0 – электрическая постоянная.
- Вектор электрического смещения (электрической индукции)
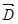 вводится формулой вводится формулой
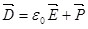 . (3.7) . (3.7)
Используя (3.6), можно записать:
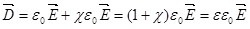 , , 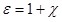 , ,
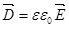 . (3.8) . (3.8)
Формула (3.8) устанавливает связь между вектором электрического смещения и напряженностью поля внутри диэлектрика.
3.3. Неполярный диэлектрик
во внешнем электрическом поле
На рис.3.2 показано расположение молекул-диполей на поверхности и внутри диэлектрика, представляющего собой прямоугольную пластину длиной L и площадью поперечного сечения S, во внешнем однородном электростатическом поле напряженности 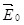 . .
Из рис.3.2 видно, что внутри происходит компенсация зарядов соседних молекул (суммарный заряд, заключенный в областях, ограниченных замкнутыми пунктирными линиями, равен нулю). Некомпенсированными остаются связанные заряды молекул на противоположных гранях диэлектрика (см.рис.3.2).
Под действием поля  молекула приобретает индуцированный дипольный момент молекула приобретает индуцированный дипольный момент 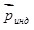 , пропорциональный , пропорциональный 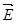 : :
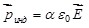 , (3.9) , (3.9)
где 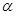 – скалярная величина, называемая поляризуемостью молекулы. – скалярная величина, называемая поляризуемостью молекулы.
Введение понятия дипольного момента молекулы позволяет описать ее поведение и соответственно поведение самого диэлектрика в электрическом поле.
На основе рис.3.2 можно получить несколько упрощенных схем диэлектрика (рис.3.3), что позволяет вывести ряд формул. Некоторые из них приведены ниже.
Электрическое поле 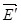 диэлектрика эквивалентно электрическому полю плоского конденсатора с поверхностной плотностью заряда его пластин, равной диэлектрика эквивалентно электрическому полю плоского конденсатора с поверхностной плотностью заряда его пластин, равной 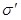 (см.рис.3.3,а). Следовательно, (см.рис.3.3,а). Следовательно,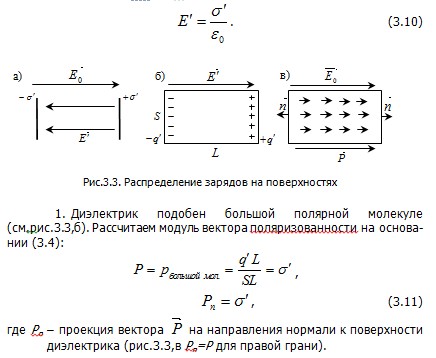
- Все индуцированные дипольные моменты молекул направлены вдоль линии
 , также направлен и вектор поляризации , также направлен и вектор поляризации 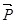 (см.рис.3.3,в). (см.рис.3.3,в).
3.4. Полярный диэлектрик
во внешнем электрическом поле
В отсутствие электрического поля дипольные моменты  полярных молекул вследствие теплового движения ориентированы хаотически и вектор поляризованности диэлектрика полярных молекул вследствие теплового движения ориентированы хаотически и вектор поляризованности диэлектрика  равен нулю (рис.3.4,а). равен нулю (рис.3.4,а).
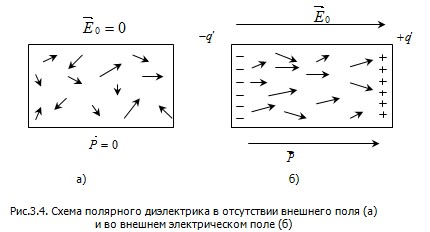
Если такой диэлектрик поместить во внешнее электрическое поле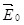 , то силы этого поля будут стремиться повернуть дипольные моменты молекул вдоль линий , то силы этого поля будут стремиться повернуть дипольные моменты молекул вдоль линий 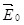 , чему препятствует тепловое движение молекул. За счет действия этих двух факторов наблюдается преимущественная ориентация дипольных моментов молекул вдоль поля (рис.3.4,б). Таким образом, диэлектрик поляризуется ( , чему препятствует тепловое движение молекул. За счет действия этих двух факторов наблюдается преимущественная ориентация дипольных моментов молекул вдоль поля (рис.3.4,б). Таким образом, диэлектрик поляризуется (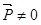 ), что сопровождается появлением связанных зарядов ), что сопровождается появлением связанных зарядов 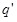 на противоположных гранях диэлектрика. на противоположных гранях диэлектрика.
3.5. Физический смысл теоремы Гаусса
для векторов 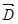 и и 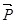
Найдем поток вектора 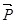 через замкнутую поверхность (она обозначена пунктирной линией на рис.3.5). На основании выражения (3.11), которое справедливо для любого диэлектрика, получим через замкнутую поверхность (она обозначена пунктирной линией на рис.3.5). На основании выражения (3.11), которое справедливо для любого диэлектрика, получим
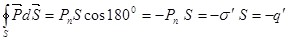 , ,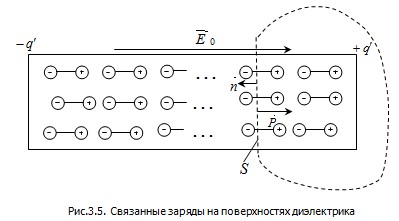
где учтено, что вектор 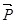 равен нулю вне диэлектрика и поэтому интеграл берется по части поверхности S, расположенной внутри диэлектрика, на этой части поверхности угол между векторами равен нулю вне диэлектрика и поэтому интеграл берется по части поверхности S, расположенной внутри диэлектрика, на этой части поверхности угол между векторами 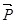 и и 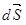 равен 1800; равен 1800; 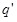 – связанный заряд внутри замкнутой поверхности S (рис.3.5). – связанный заряд внутри замкнутой поверхности S (рис.3.5).
Можно показать, что полученный результат справедлив и в общем случае. Из формулы (3.12) следует, что источником вектора 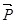 являются связанные заряды. В этом и заключается физический смысл теоремы Гаусса для вектора являются связанные заряды. В этом и заключается физический смысл теоремы Гаусса для вектора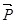 . .
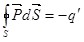 . (3.12) . (3.12)
Для вектора электрической индукции 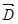 в соответствии с формулами (3.7) и (3.11) запишем: в соответствии с формулами (3.7) и (3.11) запишем: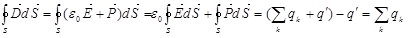
,
где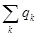 - сумма сторонних зарядов, находящихся внутри поверхности S - сумма сторонних зарядов, находящихся внутри поверхности S
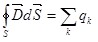 . (3.13) . (3.13)
Формула (3.13) выражает теорему Гаусса для вектора 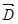 : поток электрического смещения через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности сторонних зарядов. Следовательно, источником поля вектора : поток электрического смещения через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности сторонних зарядов. Следовательно, источником поля вектора 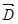 являются свободные заряды. являются свободные заряды.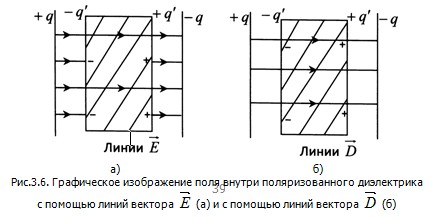
Расчет электрического поля существенно упрощается, если ввести вектор 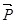 , обусловленный распределением связанных зарядов , обусловленный распределением связанных зарядов 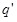 (3.12), и вектор (3.12), и вектор 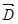 , связанный с распределением свободных зарядов q (3.13). Тот факт, что источником поля вектора , связанный с распределением свободных зарядов q (3.13). Тот факт, что источником поля вектора 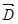 являются только свободные заряды, проводит к тому, что линии являются только свободные заряды, проводит к тому, что линии 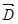 на границе диэлектрика, где появляются связанные заряды на границе диэлектрика, где появляются связанные заряды 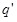 , не прерываются. Это удобно для графического изображения электрического поля в присутствии диэлектрика. На рис.3.6 в качестве примера приведено графическое изображение с помощью линий , не прерываются. Это удобно для графического изображения электрического поля в присутствии диэлектрика. На рис.3.6 в качестве примера приведено графическое изображение с помощью линий 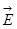 и линий и линий 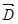 электрического поля плоского конденсатора, внутри которого находится прямоугольная пластина из диэлектрика с относительной диэлектрической проницаемостью E. электрического поля плоского конденсатора, внутри которого находится прямоугольная пластина из диэлектрика с относительной диэлектрической проницаемостью E.
Выведем формулы, связывающие свободные заряды q и их поверхностную плотность 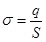 на пластинах конденсатора со связанными зарядами q на пластинах конденсатора со связанными зарядами q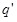 и их поверхностной плотностью и их поверхностной плотностью 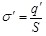 на диэлектрике. Для этого запишем для модуля напряженности на диэлектрике. Для этого запишем для модуля напряженности 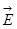 электрического поля внутри пластины (см.рис.3.6,а) в соответствии с выражениями (3.2) и (3.3): электрического поля внутри пластины (см.рис.3.6,а) в соответствии с выражениями (3.2) и (3.3):
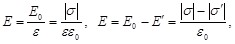
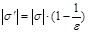 (3.14) (3.14)
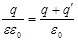 (3.15) (3.15)
В формуле (3.15) не выделены явно знаки зарядов q и 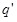 , они могут быть как больше, так и меньше нуля. Но если q>0, то тогда , они могут быть как больше, так и меньше нуля. Но если q>0, то тогда 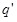 <0, и наоборот (это соответствует факту ослабления внешнего поля внутри диэлектрика). <0, и наоборот (это соответствует факту ослабления внешнего поля внутри диэлектрика).
Выражение (3.15) используется для выяснения физического смысла теоремы Гаусса для вектора 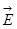 электростатического поля: источником вектора электростатического поля: источником вектора 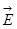 являются свободные и связанные заряды. Поэтому часть линий являются свободные и связанные заряды. Поэтому часть линий 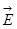 на границе диэлектрика прерывается и может изменять свое направление. на границе диэлектрика прерывается и может изменять свое направление.
Из двух векторов и 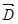 , описывающих электростатическое поле, вектор , описывающих электростатическое поле, вектор 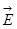 является истинным вектором этого поля, так как источником является истинным вектором этого поля, так как источником 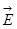 являются все существующие в природе электрические заряды, а вектор являются все существующие в природе электрические заряды, а вектор 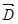 – вспомогательный вектор, служащий для упрощения расчета электрического поля в присутствии диэлектрика. – вспомогательный вектор, служащий для упрощения расчета электрического поля в присутствии диэлектрика. |
|
|

