1. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ
1.1. Электрический заряд, атомистичность заряда,
элементарный заряд
Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Причем заряды существуют двух знаков: условно называемые положительными и отрицательными.
Электрический заряд является неотъемлемым свойством некоторых элементарных частиц. Заряд всех элементарных частиц (если он не равен нулю) одинаков по абсолютной величине. Его называют элементарным зарядом. Положительный элементарный заряд обозначают +е, отрицательный – –е.
К числу элементарных частиц принадлежат, в частности, электрон (несущий отрицательный заряд -е), протон (несущий положительный заряд +е) и нейтрон (заряд которого равен нулю). Из этих частиц построены атомы и молекулы любого вещества, поэтому электрические заряды входят в состав всех тел. Обычно частицы, несущие заряды разных знаков, присутствуют в равных количествах и распределены в теле с одинаковой плотностью. В этом случае алгебраическая сумма зарядов в любом элементарном объёме тела равна нулю, и каждый такой объём (и тело в целом) будет нейтральным. По ряду причин от атома могут отрываться, наименее прочно связанные с ядром, электроны и присоединяться к другим атомам. Атомы, лишившиеся электронов, называются положительными ионами. Наоборот, атомы, присоединившие к себе лишние электроны, называются отрицательными ионами. Если, например, потереть стеклянную палочку о бумагу, то атомы стекла потеряют электроны и палочка зарядится положительно, бумага - отрицательно.
Поскольку всякий заряд q образуется совокупностью элементарных зарядов, он является целым кратным е :
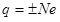 . (1.1) . (1.1)
Однако электрический заряд настолько мал, что возможную величину макроскопических зарядов можно считать изменяющейся непрерывно.
Если физическая величина может принимать только определённые дискретные значения, говорят, что эта величина квантуется. Факт, выражаемый формулой (1.1), означает, что электрический заряд квантуется.
Величина заряда, измеряемая в различных инерциальных системах отсчёта, оказывается одинаковой. Следовательно, электрический заряд является релятивистки инвариантным. Отсюда вытекает, что величина заряда не зависит от того, движется этот заряд или покоится.
В СИ электрический заряд измеряют в кулонах (Кл). Однако, несмотря на то, что первое понятие в электричестве, с которым мы встретились это заряд, единица измерения заряда Кулон (Кл) в СИ не является основной. Четвертой основной единицей в СИ (наряду с метром, килограммом и секундой) является единица силы тока 1 Ампер (А). При этом 1 Кл это такое количество электричества, которое протекает через поперечное сечение проводника за 1 секунду, при силе тока в 1 Ампер 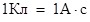 . .
Сравнительно недавно была высказана гипотеза о существовании в природе частиц с зарядом, равным 1/3 элементарного, так называемых кварков. Предполагают, что из кварков состоят протоны, нейтроны и другие, относительно тяжелые частицы. Однако обнаружить кварки экспериментально пока не удалось.
1.2. Закон сохранения заряда
Электрические заряды могут исчезать и возникать вновь. Однако всегда возникают или исчезают два элементарных заряда противоположных знаков. Например, электрон и позитрон (положительный электрон) при встрече аннигилируют, т.е. превращаются в нейтральные гамма-фотоны. При этом исчезают заряды -е и +е. В ходе процесса, называемого рождением пары, гамма-фотон, попадая в поле атомного ядра, превращается в пару частиц – электрон и позитрон, при этом возникают заряды -е и +е.
Таким образом, суммарный заряд электрически изолированной системы не может изменяться. Это утверждение носит название закона сохранения электрического заряда.
Отметим, что закон сохранения электрического заряда тесно связан с релятивисткой инвариантностью заряда. Действительно, если бы величина заряда зависела от его скорости, то, приведя в движение заряды одного какого-то знака, мы изменили бы суммарный заряд изолированной системы.
1.3. Закон Кулона
Заряженные тела взаимодействуют друг с другом, причем одноименные заряды отталкиваются, а разноименные притягиваются.
Точное математическое выражение закона этого взаимодействия в 1785 г. установил французский физик Ш.Кулон. С тех пор закон взаимодействия неподвижных электрических зарядов носит его имя.
Заряженное тело, размерами которого можно пренебречь, по сравнению с расстоянием между взаимодействующими телами может быть принято за точечный заряд. Кулон в результате своих опытов установил, что:
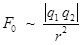 . .
Сила взаимодействия в вакууме двух неподвижных точечных зарядов прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними. Индекс «0» у силы показывает, что это сила взаимодействия зарядов в вакууме.
Установлено, что закон Кулона справедлив на расстояниях от  до нескольких километров. до нескольких километров.
Чтобы поставить знак равенства, необходимо ввести некоторый коэффициент пропорциональности, величина которого зависит от выбора системы единиц:
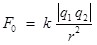 . .
Уже отмечалось, что в СИ заряд измеряется в Кл. В законе Кулона известна размерность левой части единица силы 1H, известна размерность правой части 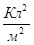 , поэтому коэффициент k получается размерным и равным , поэтому коэффициент k получается размерным и равным 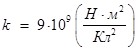 . Однако в СИ этот коэффициент пропорциональности принято записывать в несколько другом виде: . Однако в СИ этот коэффициент пропорциональности принято записывать в несколько другом виде:
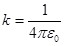 , (1.2) , (1.2)
следовательно, 
или ,
где Ф (фарад) – единица электрической емкости (см. п. 3.3).
Величину 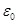 называют электрической постоянной. Это действительно фундаментальная постоянная, фигурирующая во многих уравнениях электродинамики. называют электрической постоянной. Это действительно фундаментальная постоянная, фигурирующая во многих уравнениях электродинамики.
Таким образом, закон Кулона в скалярной форме имеет вид:
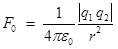 . .
Закон Кулона может быть выражен в векторной форме:
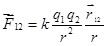 , (1.3) , (1.3)
где 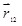 ? радиус-вектор, соединяющий заряд q2 с зарядом q1, ? радиус-вектор, соединяющий заряд q2 с зарядом q1, 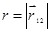 ; ; 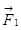 сила, действующая на заряд q1со стороны заряда q2. На заряд q2 со стороны заряда q1 действует сила сила, действующая на заряд q1со стороны заряда q2. На заряд q2 со стороны заряда q1 действует сила 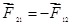 (рис.1.1). (рис.1.1).
Рис.1.1. К закону Кулона в векторной форме
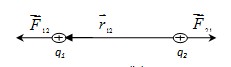
Опыт показывает, что сила взаимодействия двух данных зарядов не изменяется, если вблизи них расположить ещё какие-либо другие заряды.
1.4. Электростатическое поле
Взаимодействие между покоящимися зарядами осуществляется через промежуточную среду и с конечной скоростью.
Впервые такая идея была высказана М.Фарадеем. Согласно его представлениям заряды не действуют друг на друга непосредственно. Каждый из них создает в окружающем пространстве электрическое поле. Поле одного заряда действует на другой и наоборот. Причем поле заряда не действует на сам заряд.
Если мы изменим положение заряда в пространстве, либо изменим его величину, то поле этого заряда также изменится. Причем изменение поля на некотором расстоянии произойдет не мгновенно c изменением положения заряда или его величины, а спустя некоторый промежуток времени. Таким образом, электрическое поле изменяется не мгновенно, а с конечной скоростью.
Эта скорость называется скоростью распространения электромагнитного взаимодействия, равна скорости света в пустоте и имеет численное значение 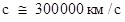 . .
Электростатическое поле – это материальная среда, так как взаимодействие между телами (зарядами) может передаваться только через материю. Будучи материальной средой поле обладает свойствами, присущими материи, а именно – массой, энергией и др.
Поле проявляет себя в том, что помещенный в какую-либо его точку электрический заряд оказывается под действием силы. Следовательно, для того, чтобы выяснить, имеется ли в данном месте электрическое поле, надо поместить туда заряженное тело («пробный» заряд).
Введем понятие напряжённости поля. Если в поле, создаваемое зарядом 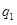 , поместить пробный точечный заряд , поместить пробный точечный заряд 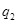 , то на него действует сила , то на него действует сила 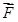 , различная в разных точках поля, которая, согласно закону Кулона (1.3), пропорциональна пробному заряду , различная в разных точках поля, которая, согласно закону Кулона (1.3), пропорциональна пробному заряду 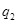 . Поэтому отношение . Поэтому отношение 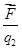 не зависит от не зависит от 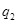 и характеризует электростатическое поле в той точке, где пробный заряд находится. и характеризует электростатическое поле в той точке, где пробный заряд находится.
Эта векторная величина называется напряженностью поля  и является силовой характеристикой электростатического поля. Чем больше напряженность поля, тем с большей силой оно действует на заряд. и является силовой характеристикой электростатического поля. Чем больше напряженность поля, тем с большей силой оно действует на заряд.
В общем случае вектор  определяется по формуле: определяется по формуле:
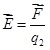 , ,
а в случае поля точечного заряда
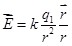 . (1.4) . (1.4)
Напряженность поля ? это физическая величина, равная отношению силы, действующей на пробный точечный заряд в данной точке поля к величине этого заряда.
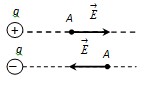 Направлен вектор Направлен вектор  вдоль радиальной прямой, проходящей через заряд q и данную точку поляA, от заряда, если он положителен, и к заряду, если он отрицателен (рис. 1.2) вдоль радиальной прямой, проходящей через заряд q и данную точку поляA, от заряда, если он положителен, и к заряду, если он отрицателен (рис. 1.2)
За единицу напряженности электрического поля принимают напряженность такого поля, в котором на заряд в 1 Кл действует сила в 1Н. В СИ эта единица называется «Ньютон на Кулон»: 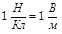 , где В (вольт) – единица потенциала электростатического поля. , где В (вольт) – единица потенциала электростатического поля.
1.5. Принцип суперпозиции электростатических полей
Если в данной точке пространства различные заряженные тела создают поля с напряженностями 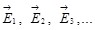 , и т.д., то результирующая напряженность поля в этой точке равна: , и т.д., то результирующая напряженность поля в этой точке равна:
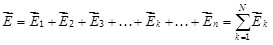 , ,
где N – число зарядов, создающих систему.
Это утверждение называют принципом суперпозиции электрических полей. Он вытекает из принципа суперпозиции сил в механике.
Покажем это на примере двух зарядов q1и q2 (рис. 1.3).
Эти заряды создают вокруг себя электрические поля с напряженностями 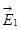 и и 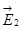 соответственно. На внесённый заряд соответственно. На внесённый заряд 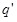 со стороны этих полей действуют силы со стороны этих полей действуют силы 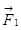 и и 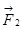 соответственно: соответственно:
 . .
Результирующая сила 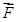 : :
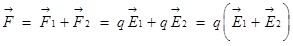 . .
Результирующая напряженность поля будет равна:
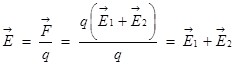 . .
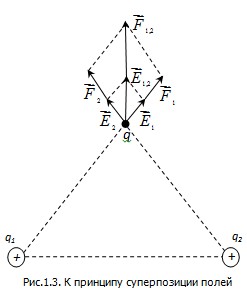
Абсолютная величина вектора  может быть рассчитана по теореме косинусов: может быть рассчитана по теореме косинусов:
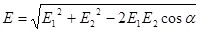 , ,
где 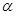 – угол между векторами – угол между векторами 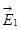 и и 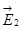 . .
Итак, если электростатическое поле создано не одним, а несколькими зарядами, то напряжённость такого поля равна векторной сумме напряжённостей полей, создаваемых в данной точке каждым из зарядов в отдельности.
1.6. Силовые линии электростатического поля
Непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с вектором напряженности, называются силовыми линиями электрического поля или линиями напряженности.
В действительности силовых линий не существует, это просто графический метод исследования электростатических полей.
Силовые линии наделены следующими свойствами:
– силовые линии электростатического поля не замкнуты ? они начинаются на положительных и заканчиваются на отрицательных зарядах;
– линии непрерывны и нигде не пересекаются (так как их пересечение означало бы отсутствие определенного направления напряженности электрического поля в данной точке);
– густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности площадки, перпендикулярной к линиям, было равно численному значению (модулю) вектора  . .
Так как силовые линии начинаются или оканчиваются на заряженных телах, а затем расходятся в разные стороны, то густота линий больше вблизи заряженных тел. Следовательно, вблизи заряженных тел напряженность поля больше, чем в более удалённых точках.
Общее число силовых линий пересекающих некоторую поверхность, иначе называют потоком вектора напряжённости поля.
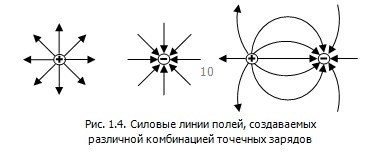
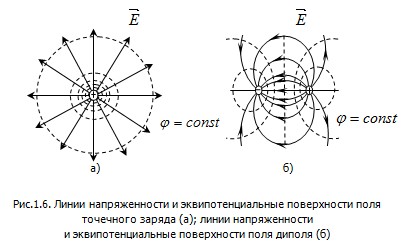
На рис.1.4 приведены силовые линии точечных положительного и отрицательного зарядов и электрического диполя (системы двух зарядов).
С графическим изображением полей, создаваемых более сложной системы зарядов, можно познакомиться в лаборатории виртуального практикума кафедры «Физика».
1.7. Эквипотенциальные поверхности
Для более наглядного графического изображения полей, кроме линий напряжённости, используют поверхности равного потенциала или эквипотенциальные поверхности. Как следует из названия, эквипотенциальная поверхность – это такая поверхность, все точки которой имеют одинаковый потенциал. Если потенциал задан как функция x, y, z, то уравнение эквипотенциальной поверхности имеет вид:
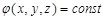 . .
Линии напряжённости поля перпендикулярны эквипотенциальным поверхностям.
Докажем это утверждение.
Пусть линия  и силовая линия составляют некоторый угол и силовая линия составляют некоторый угол 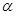 (рис.1.5). (рис.1.5).
Переместим из точки 1 в точку 2 вдоль линии 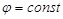 пробный заряд пробный заряд 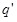 . При этом силы поля совершают работу: . При этом силы поля совершают работу:
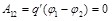 . (1.5) . (1.5)
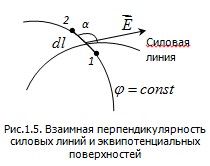 То есть работа перемещения пробного заряда вдоль эквипотенциальной поверхности равна нулю. Эту же работу можно определить и другим способом – как произведение заряда То есть работа перемещения пробного заряда вдоль эквипотенциальной поверхности равна нулю. Эту же работу можно определить и другим способом – как произведение заряда  на модуль напряженности на модуль напряженности  поля, действующего на пробный заряд, на величину перемещения поля, действующего на пробный заряд, на величину перемещения 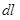 и на косинус угла между вектором и на косинус угла между вектором  и вектором перемещения и вектором перемещения 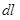 , т.е. косинус угла , т.е. косинус угла 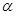 (см.рис.1.5): (см.рис.1.5):
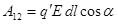 . .
Величина работы не зависит от способа её подсчёта, согласно (1.5) она равна нулю. Отсюда вытекает, что 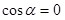 и, соответственно, и, соответственно, 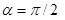 , что и требовалось доказать. , что и требовалось доказать.
Эквипотенциальную поверхность можно провести через любую точку поля. Следовательно, таких поверхностей может быть построено бесконечное множество. Условились, однако, проводить поверхности таким образом, чтобы разность потенциалов для двух соседних поверхностей была бы всюду одна и та же. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряжённости поля. Действительно, чем гуще располагаются эквипотенциальные поверхности, тем быстрее изменяется потенциал при перемещении вдоль нормали к поверхности.
На рис.1.6,а показаны эквипотенциальные поверхности (точнее, их пересечения с плоскостью чертежа) для поля точечного заряда. В соответствии с характером изменения  эквипотенциальные поверхности при приближении к заряду становятся гуще. На рис.1.6,б изображены эквипотенциальные поверхности и линии напряжённости для поля диполя. Из рис.1.6 видно, что при одновременном использовании эквипотенциальных поверхностей и линий напряжённости картина поля получается особенно наглядной. эквипотенциальные поверхности при приближении к заряду становятся гуще. На рис.1.6,б изображены эквипотенциальные поверхности и линии напряжённости для поля диполя. Из рис.1.6 видно, что при одновременном использовании эквипотенциальных поверхностей и линий напряжённости картина поля получается особенно наглядной.
Для однородного поля эквипотенциальные поверхности, очевидно, представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению напряжённости поля.
1.8. Связь между напряжённостью поля и потенциалом
(градиент потенциала)
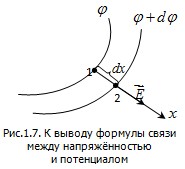 Пусть имеется произвольное электростатическое поле. В этом поле проведём две эквипотенциальные поверхности таким образом, что они отличаются одна от другой потенциалом на величину dφ (рис. 1.7) Пусть имеется произвольное электростатическое поле. В этом поле проведём две эквипотенциальные поверхности таким образом, что они отличаются одна от другой потенциалом на величину dφ (рис. 1.7)
Вектор напряжённости направлен по нормали к поверхности 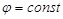 . Направление нормали совпадает с направлением оси x. Ось x, проведённая из точки 1, пересекает поверхность . Направление нормали совпадает с направлением оси x. Ось x, проведённая из точки 1, пересекает поверхность 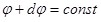 в точке 2. в точке 2.
Отрезок dx представляет собой кратчайшее расстояние между точками 1 и 2. Работа, совершаемая при перемещении заряда 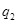 вдоль этого отрезка: вдоль этого отрезка:
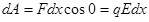 . .
С другой стороны, эту же работу можно записать как:
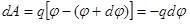 . .
Приравнивая эти два выражения, получаем:
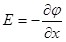 , (1.6) , (1.6)
где символ частной производной подчёркивает, что дифференцирование производиться только по x. Повторив аналогичные рассуждения для осей yи z, можем найти вектор  : :
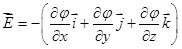 , (1.7) , (1.7)
где 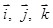 – единичные векторы координатных осей x, y, z. – единичные векторы координатных осей x, y, z.
Вектор, определяемый выражением (1.7), называется градиентом скаляра φ. Для него наряду с обозначением 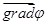 применяется также обозначение применяется также обозначение 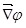 . . 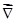 («набла») означает символический вектор, называемый оператором Гамильтона («набла») означает символический вектор, называемый оператором Гамильтона
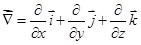 . .
Следовательно, из определения градиента можно записать:
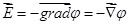 , ,
т.е. напряжённость поля  равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряжённости равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряжённости  поля направлен в сторону убывания потенциала. поля направлен в сторону убывания потенциала.
По формуле (1.7) можно найти проекцию вектора  на выбранное направление в пространстве, например, на ось x: на выбранное направление в пространстве, например, на ось x:
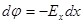 или или 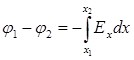 , (1.8) , (1.8)
где (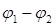 ) − разность потенциалов между точками 1 и 2, расположенными на оси x. ) − разность потенциалов между точками 1 и 2, расположенными на оси x.
1.9. Работа, совершаемая при перемещении заряда
в электростатическом поле. Теорема о циркуляции
вектора напряжённости электростатического поля
Предположим, что некоторый точечный заряд 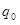 перемещается в поле неподвижного точечного заряда перемещается в поле неподвижного точечного заряда  из точки 1 в точку 2 (рис.1.8). На заряд действует сила, и, следовательно, совершается работа. Первоначально определим работу на малом перемещении из точки 1 в точку 2 (рис.1.8). На заряд действует сила, и, следовательно, совершается работа. Первоначально определим работу на малом перемещении 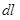 : :
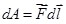 или или 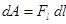 , ,
где 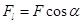 – проекция вектора силы – проекция вектора силы  на направление перемещения на направление перемещения 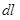 . .
Следовательно, 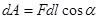 , но , но 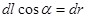 , где dr равно приращению модуля радиуса-вектора dr, поэтому , где dr равно приращению модуля радиуса-вектора dr, поэтому 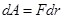 . Так как заряды точечные, то . Так как заряды точечные, то
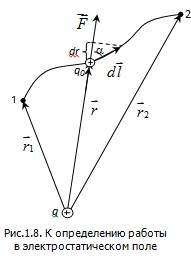 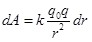 . .
Работа, совершаемая при перемещении заряда 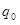 из точки 1 в точку 2, определяется выражением: из точки 1 в точку 2, определяется выражением:
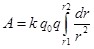 (1.9) (1.9)
или после интегрирования
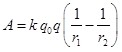 . (1.10) . (1.10)
Из выражения (1.10) можно сделать следующие выводы:
– работа не зависит от формы траектории, по которой движется заряд q0,, зависит от положения начальной 1 и конечной 2 точек перемещения. Силовые поля, удовлетворяющие этому условию, называют потенциальными, а силы, действующие в этих полях называют консервативными. Следовательно, электростатическое поле потенциально, а силы в этом поле консервативны;
– работа, совершаемая при перемещении заряда q0 вдоль замкнутой траектории (r1 = r2), равна нулю.
Если силовые линии замкнуты, то такое поле называется вихревым. К таким полям относятся магнитное и возбуждаемое переменным магнитным – электрическое.
Работу, совершаемую при перемещении заряда в поле вдоль замкнутого контура, можно определить выражением:
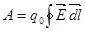 , так как , так как 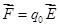 . .
Согласно выражению (1.8) эта работа равна нулю и, следовательно,
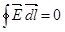 . (1.11) . (1.11)
Выражение 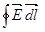 называют циркуляцией вектора напряжённости электростатического поля, а (1.11) теоремой о циркуляции называют циркуляцией вектора напряжённости электростатического поля, а (1.11) теоремой о циркуляции  . .
Выражение (1.11) позволяет решать многие задачи, связанные с электростатическим полем.
1.10. Энергия заряда в электростатическом поле.Потенциал. Разность потенциалов
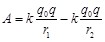 , ,
учитывая, что 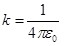 , получаем , получаем
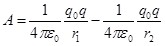 . (1.12) . (1.12)
Известно, что работа связана с потенциальной энергией выражением:
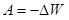 . .
Систему в данном случае составляют заряд и поле либо можно рассматривать систему, состоящую из двух зарядов q0 и q.
Из (1.12) следует, что
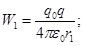 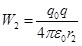 , ,
где W1 – энергия системы в первом состоянии; W2 – энергия системы во втором состоянии. При произвольном расстоянии между зарядами:
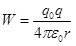 . (1.13) . (1.13)
Потенциал  в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Потенциал является величиной скалярной и определяется по формуле: в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Потенциал является величиной скалярной и определяется по формуле:
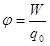 . (1.14) . (1.14)
В СИ потенциал измеряется в вольтах (В). За единицу потенциала в 1 В принимается потенциал такой точки поля, в которой заряд в 1 Кл обладает энергией в 1 Дж.
Из уравнений (1.13) и (1.14) очевидно, что потенциал поля, создаваемого точечным зарядом q, определяется выражением:
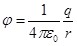 , (1.15) , (1.15)
где Q – заряд, который создаёт поле; Y – расстояние от заряда q до точки, где определяется потенциал.
Предположим, что заряд Q0 находится в точке 1 электростатического поля, потенциал которой равен 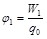 . После его перемещения в точку 2 совершается работа . После его перемещения в точку 2 совершается работа
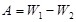 , ,
где 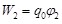 – потенциальная энергия системы заряд-поле для точки 2; – потенциальная энергия системы заряд-поле для точки 2; 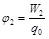 – потенциал поля в точке 2. – потенциал поля в точке 2.
Разность потенциалов между точками 1 и 2:
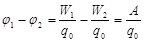 . (1.16) . (1.16)
Из (1.16) следует, что разность потенциалов между двумя точками электростатического поля определяется отношением работы, совершаемой силами поля, при перемещении заряда из одной точки в другую, к величине этого заряда.
1.11. Поток вектора напряженности. Теорема Гаусса
Предположим, что имеется однородное электростатическое поле, в котором расположен плоский контур площадью S (рис.1.9). Под потоком 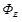 вектора вектора 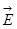 , пронизывающим площадку S, понимают произведение напряженности поля на площадь контура и на косинус угла , пронизывающим площадку S, понимают произведение напряженности поля на площадь контура и на косинус угла 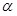 между вектором напряженности и нормалью к контуру. Для однородного поля: между вектором напряженности и нормалью к контуру. Для однородного поля:
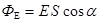 . .
Поток может принимать положительное значение, если угол 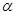 острый, и отрицательное, если угол острый, и отрицательное, если угол 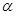 тупой. При тупой. При 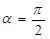 поток равен нулю. Учитывая, что поток равен нулю. Учитывая, что 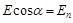 , где , где  - проекция вектора напряженности на направление нормали, - проекция вектора напряженности на направление нормали, 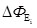 можно определить выражением: можно определить выражением:
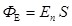 . (1.17) . (1.17)
Если поле неоднородное, а контур не плоский, то для определения потока необходимо контур мысленно разделить на малые элементы площади. В пределах каждой такой площади поле можно принимать за однородное, а сам элемент площади за плоский. Поток, связанный с одним из элементов, 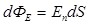 , а со всей поверхностью: , а со всей поверхностью:
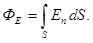 (1.18) (1.18)
Выражение (1.18) является наиболее общим определением потока вектора напряженности поля. Кроме того, поток может быть определен как общее число силовых линий, пронизывающих поверхность.
Определим поток через сферическую поверхность Si, в центре которой расположен точечный заряд q (рис.1.10).
В силу центральной симметрии напряженность поля в каждой точке поверхности одинакова по модулю и может быть определена по формуле (1.4), тогда выражение (1.17), учитывая, что 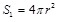 , примет вид: , примет вид:
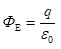 . .
Можно сделать выводы:
- поток вектора
 не зависит от радиуса сферы; не зависит от радиуса сферы;
- при перемещении заряда внутри сферы поток вектора
 не изменяется, так как общее число линий напряженности поля, пересекающих данную поверхность, остается прежним. По этой же причине при замене сферической поверхности на любую произвольную замкнутую поверхность поток не меняется; не изменяется, так как общее число линий напряженности поля, пересекающих данную поверхность, остается прежним. По этой же причине при замене сферической поверхности на любую произвольную замкнутую поверхность поток не меняется;
- если поверхность S1 (см.рис.1.10) не охватывает заряд, то поток вектора
 будет равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий выходящих. будет равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий выходящих.
Если внутри замкнутой поверхности расположено N зарядов, то поток 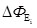 от произвольного заряда qk: от произвольного заряда qk:
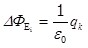 , (1.19), , (1.19),
где qk – значение k-го заряда.
Просуммировав значение потоков в формуле (1.18) получим:
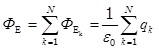 . (1.20) . (1.20)
Так как суммарный поток  через замкнутую поверхность определяется выражением (1.17), то, приравняв правые части формул (1.17) и (1.20),получим: через замкнутую поверхность определяется выражением (1.17), то, приравняв правые части формул (1.17) и (1.20),получим:
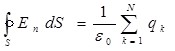 . (1.21) . (1.21)
Полученное выражение (1.21) называется теоремой Гаусса. Согласно этой теореме поток вектора напряженности электростатического поля в вакууме через замкнутую поверхность любой формы равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленных на 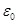 . .
Применение теоремы Гаусса для произвольного распределения зарядов может столкнуться с математическими трудностями, однако в случаях, обладающих симметрией, многие задачи решаются просто.
При решении подобных задач используют понятие объемной плотности заряда 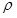 , определяемого по формуле: , определяемого по формуле:
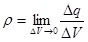 . .
При равномерном распределении заряда qпо объему V:
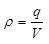 . .
Кроме того, используют понятия  поверхностной и линейной поверхностной и линейной  плотностей зарядов, определяемых соответственно по формулам: плотностей зарядов, определяемых соответственно по формулам:
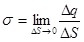 ; (1.22) ; (1.22)
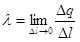 . (1.23) . (1.23)
При равномерном распределении зарядов:
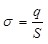 ; (1.24) ; (1.24)
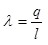 . (1.25) . (1.25)
Зная плотности, можно определить величину зарядов, заключенных внутри поверхностей.
Теорема Гаусса позволяет решать две задачи: 1) определение распределения напряженности поля при известном распределении зарядов и 2) определение распределения зарядов по заданному распределению напряженности.
1.12. Применение теоремы Гаусса
для расчета электростатических полей
В случае электростатических полей, обладающих симметрией (плоской, осевой или сферической), теорема Гаусса позволяет достаточно просто получить выражение для определения модуля вектора  . Для этого достаточно теорему применять по следующей схеме: . Для этого достаточно теорему применять по следующей схеме:
- в каждой точке поля из симметрии поставленной задачи определяют направление вектора
 ; ;
- выбирают замкнутую поверхность (поверхность интегрирования) и определяют поток вектора
 через неё. Выбранная поверхность должна отражать симметрию поля, и внутри неё должен находиться заряд (или часть заряда); через неё. Выбранная поверхность должна отражать симметрию поля, и внутри неё должен находиться заряд (или часть заряда);
- определяют величину заряда, заключенного внутри поверхности;
- применяют теорему Гаусса (1. 21).
1.12.1. Поле равномерно заряженной
бесконечно протяженной плоскости
Так как плоскость заряжена равномерно, то во всех её точках поверхностная плотность зарядов  одинакова, поэтому поле такой плоскости однородно. Линии вектора одинакова, поэтому поле такой плоскости однородно. Линии вектора  перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны (рис.1.11,а). перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны (рис.1.11,а).
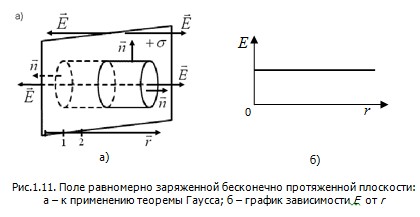
Выбираем замкнутую цилиндрическую поверхность, основания которой параллельны заряженной плоскости, а ось перпендикулярна ей. В таком случае линии вектора напряженности пересекают только два основания поверхности, поток через которые согласно (1.18) может быть определен:
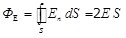 , ,
где S – площадь основания поверхности.
Определяем заряд внутри цилиндрической поверхности, используя (1.24).
Применяем теорему Гаусса (1.21):
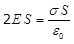 , откуда , откуда 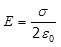 . (1.25) . (1.25)
На рис.1.11,б приведен график зависимости модуля вектора  в зависимости от в зависимости от  , где , где  - расстояние от плоскости до точки, в которой определяется значение - расстояние от плоскости до точки, в которой определяется значение  . .
Используя связь между напряженностью и потенциалом поля (1.7), можно определить разность потенциалов между двумя точками поля, расположенными на расстоянии  и и  от плоскости (см.рис.1.11,а) от плоскости (см.рис.1.11,а)
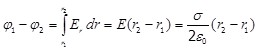 . .
В заключение отметим, что реальная плоскость может быть принята за бесконечно протяженную при условии, что её размеры значительно больше расстояния от неё до точек, в которых определяется напряженность.
1.12.2. Поле плоского конденсатора
Используя выражение (1.26) и принцип суперпозиции полей, можно определить напряженность поля плоского конденсатора (рис.1.12). Из построения силовых линий (см.рис.1.12,а) следует, что поле вне пластин отсутствует (слева и справа от пластин линии напряженности  и и  направлены навстречу друг другу), а внутри конденсатора: направлены навстречу друг другу), а внутри конденсатора:
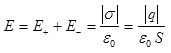 , ,
где  – модуль заряда пластины; S – площадь пластины. – модуль заряда пластины; S – площадь пластины.
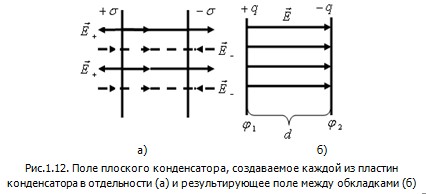
Разность потенциалов (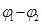 ) (иначе напряжение U) между пластинами определим согласно (1.8): ) (иначе напряжение U) между пластинами определим согласно (1.8):
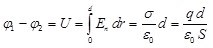 , (1.27) , (1.27)
где d- расстояние между пластинами.
Приведенные расчеты справедливы при условии, что расстояние между пластинами значительно меньше размеров пластин.
1.12.3. Поле равномерно заряженной
бесконечно длинной прямой нити
Для равномерно заряженной нити во всех её точках линейная плотность заряда 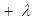 будет одинаковой, поэтому поле имеет осевую симметрию: линии вектора будет одинаковой, поэтому поле имеет осевую симметрию: линии вектора  представляют собой прямые, выходящие из нити и лежащие в плоскостях, перпендикулярных к ней (рис.1.13,а). На одинаковых расстояниях от нити, т.е. на цилиндрической поверхности модуль представляют собой прямые, выходящие из нити и лежащие в плоскостях, перпендикулярных к ней (рис.1.13,а). На одинаковых расстояниях от нити, т.е. на цилиндрической поверхности модуль  будет одинаковым. будет одинаковым.
Поверхность интегрирования выбирают цилиндрическую, ось которой совпадает с нитью. Поток вектора  через основания цилиндра равен нулю (линии напряженности их не пересекают), поэтому остается поток только через боковую поверхность и согласно (1.18) получим: через основания цилиндра равен нулю (линии напряженности их не пересекают), поэтому остается поток только через боковую поверхность и согласно (1.18) получим:
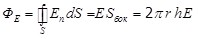 , ,
где r – радиус цилиндра (расстояние от нити до точки, где определяется напряженность); h – высота цилиндрической поверхности.
Определяем заряд внутри цилиндрической поверхности:
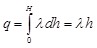 . .
Применяем теорему Гаусса (1.21):
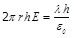 , откуда , откуда 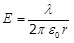 . .
На (рис.1.13,б) приведен график зависимости модуля вектора  от расстояния от нити до точки, в которой он определяется. от расстояния от нити до точки, в которой он определяется.
Используя связь между потенциалом и напряженностью поля (1.7), можно определить разность потенциалов между двумя точками поля, находящимися на расстояниях r1 и r2 от нити (см.рис.1.13,а):
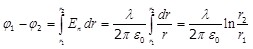 . .
В заключение отметим, что приведенные выводы справедливы для нити конечной длины при условии, что её длина значительно больше расстояния от нити до точки, в которой определяется напряженность.
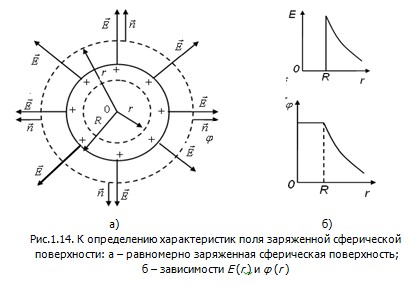
1.12.4. Поле равномерно заряженной сферической поверхности радиуса R и заряда q
Поле сферической поверхности обладает центральной симметрией – линии вектора  представляют собой прямые, выходящие из поверхности, перпендикулярные к ней (рис.1.14). Вне сферы на одинаковых расстояниях от ее центра модуль вектора представляют собой прямые, выходящие из поверхности, перпендикулярные к ней (рис.1.14). Вне сферы на одинаковых расстояниях от ее центра модуль вектора  будет одинаковым. будет одинаковым.
Поверхность интегрирования выбираем в виде сферы, центр которой совпадает с центром заряженной сферы (точка О) и имеющей радиус r. Поток вектора  через эту сферу (1.18): через эту сферу (1.18):
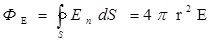 ; ; 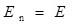 . .
Если 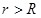 , внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле и по теореме Гаусса (1.21): , внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле и по теореме Гаусса (1.21):
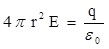 , откуда , откуда 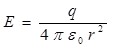 , ,
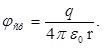
Если 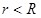 , то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует. , то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует.
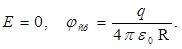
- Если r=R справедливы следующие равенства:
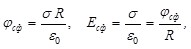
где  - поверхностная плотность заряда, согласно (1.24): - поверхностная плотность заряда, согласно (1.24):
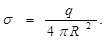
 Таким образом, можно сделать вывод, что внутри сферы поле отсутствует, а за её пределами оно совпадает с полем точечного заряда q, помещенного в центр сферы. Таким образом, можно сделать вывод, что внутри сферы поле отсутствует, а за её пределами оно совпадает с полем точечного заряда q, помещенного в центр сферы.
Графики зависимости E и  от r, где r- расстояние от центра сферы до точки, в которой определяются напряженность и потенциал поля, приведены на рис.1.14,б. от r, где r- расстояние от центра сферы до точки, в которой определяются напряженность и потенциал поля, приведены на рис.1.14,б.
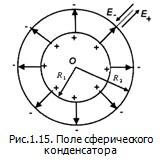
С помощью принципа суперпозиции легко определить поле двух сферических поверхностей, имеющих общий центр (точка O, рис.1.15), которые заряжены одинаковыми по величине, но различными по знаку зарядами. Такая система называется сферическим конденсатором. В общей внутренней части меньшей и большей сфер поле отсутствует. В зазоре между поверхностями напряженность поля Е определяется по формуле:
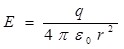 , ,
где 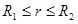 . .
Разность потенциалов между сферами определяется по формуле (1.8):
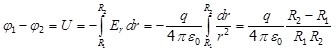 . .
Поле сферического конденсатора в отличие от поля плоского является неоднородным.
1.12.5. Поле объемно-заряженного шара
с равномерной плотностью заряда
Пусть шар радиуса R заряжен с постоянной объемной плотностью 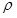 . Поле в этом случае обладает центральной симметрией. Легко сообразить, что для поля вне шара получается тот же результат, что и в случае заряженной сферы. Однако для точек внутри шара результат будет иным. Сферическая поверхность радиуса r( . Поле в этом случае обладает центральной симметрией. Легко сообразить, что для поля вне шара получается тот же результат, что и в случае заряженной сферы. Однако для точек внутри шара результат будет иным. Сферическая поверхность радиуса r(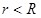 ) заключает в себе заряд равный: ) заключает в себе заряд равный: 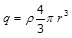 . Поэтому теорему Гаусса (1.21) для такой поверхности запишем следующим образом: . Поэтому теорему Гаусса (1.21) для такой поверхности запишем следующим образом:
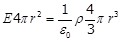 . .
Отсюда, заменив 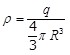 , получим , получим
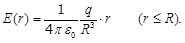
Таким образом, внутри шара напряженность поля растет линейно с расстоянием r от центра шара. Вне шара напряженность убывает по такому же закону, как и у поля точечного заряда. В центре шара 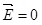 . . |
|
|

