|
4. ОСНОВЫ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ТВЕРДОГО ТЕЛА
4.1. Момент инерции
При вращении твердого тела вокруг неподвижной оси отдельные точки тела описывают окружности, центры которых лежат на оси вращения. Основы кинематики вращательного движения были изложены в разделе 1.5.
Для описания вращательного движения твердого тела вводят понятие момента инерции.
Моментом инерции I материальной точки называется скалярная физическая величина, определяемая произведением ее массы 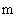 на квадрат радиуса окружности на квадрат радиуса окружности 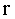 , по которой она может двигаться относительно некоторой произвольно выбранной оси ОО‛ (рис.4.1,а) , по которой она может двигаться относительно некоторой произвольно выбранной оси ОО‛ (рис.4.1,а)
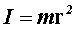 . .
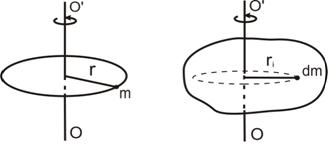
а) б)
Рис.4.1. К определению понятия момента инерции
Если твердое тело, вращающееся относительно некоторой произвольно выбранной оси ОО', представить в виде системы материальных точек массой 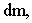 и просуммировать моменты инерции этих так называемых элементарных масс, то получим момент инерции всего тела и просуммировать моменты инерции этих так называемых элементарных масс, то получим момент инерции всего тела
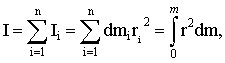
где 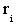 – радиус вращения i–й элементарной массы, а интеграл берется по всему объему тела (рис. 4.1,б). Для однородных тел, для которых плотность – радиус вращения i–й элементарной массы, а интеграл берется по всему объему тела (рис. 4.1,б). Для однородных тел, для которых плотность 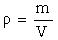 (где (где 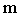 – масса тела, а – масса тела, а 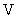 – его объем, т.е. плотность определяется массой, заключенной в единице объема), момент инерции будет вычисляться по формуле – его объем, т.е. плотность определяется массой, заключенной в единице объема), момент инерции будет вычисляться по формуле
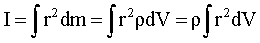 , т.е. , т.е. 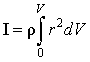 . .
Ниже приведены значения моментов инерции для некоторых однородных тел правильной формы с массой 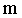 относительно оси, проходящей через центр масс тела. относительно оси, проходящей через центр масс тела.
Таблица 2
Моменты инерции тел правильной формы
|
Тело
|
Положение оси
вращения
|
Момент
инерции
|
|
Полый тонкостенный
цилиндр радиусом R
|
Ось симметрии
|
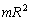
|
|
Сплошной цилиндр
или диск радиусом R
|
Ось симметрии
|
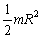
|
|
Прямой тонкий
стержень длиной l
|
Ось перпендикулярна
стержню и проходит
через его середину
|
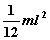
|
|
Шар радиусом R
|
Ось проходит через
центр шара
|
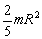
|
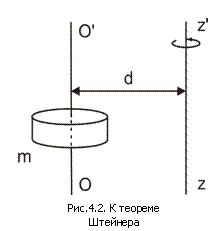 Для определения момента инерции тела относительно произвольной оси используется теорема Штейнера. Для определения момента инерции тела относительно произвольной оси используется теорема Штейнера.
Теорема Штейнера: если известен момент инерции тела относительно оси ОО', проходящей через центр масс тела (обозначим его Io), то момент инерции тела
относительно любой параллельной ей оси ZZ' (обозначим его 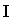 ) равен ) равен
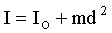 , ,
где 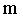 – масса тела; d – расстояние между осями (рис.4.2). – масса тела; d – расстояние между осями (рис.4.2).
4.2. Кинетическая энергия вращающегося твердого тела
Кинетическая энергия измеряется работой, которую тело может произвести благодаря инерции при затормаживании тела до полной остановки. При вращательном движении роль массы 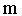 выполняет момент инерции выполняет момент инерции 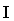 , а вместо линейной скорости , а вместо линейной скорости 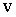 выступает угловая скорость выступает угловая скорость 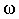 , и формула кинетической энергии при вращательном движении тела вокруг неподвижной оси приобретает вид: , и формула кинетической энергии при вращательном движении тела вокруг неподвижной оси приобретает вид:
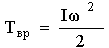 . .
В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, кинетическая энергия складывается из энергии поступательного движения и энергии вращения:
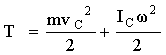 , ,
где 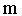 - масса катящегося тела; - масса катящегося тела; 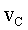 - скорость центра масс тела; - скорость центра масс тела;
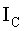 - момент инерции тела относительно оси, проходящей через его центр масс; - момент инерции тела относительно оси, проходящей через его центр масс; 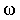 - угловая скорость тела. - угловая скорость тела.
4.3. Момент силы. Уравнение динамики
вращательного движения твердого тела
Моментом силы 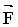 относительно неподвижной точки О относительно неподвижной точки О
называется векторная физическая величина, определяемая векторным произведением радиус-вектора 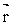 , проведенного из точки О в точку А приложения силы, на силу , проведенного из точки О в точку А приложения силы, на силу 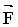 (рис.4.3): (рис.4.3):
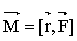 . .
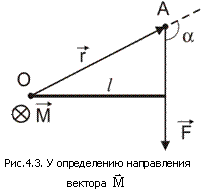 Модуль момента силы равен Модуль момента силы равен 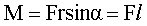 , где , где 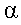 – угол между – угол между 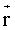 и и 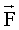 , , 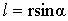 - плечо силы - плечо силы 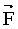 (l – длина перпендикуляра, опущенного из точки О на направление действия силы (см. рис. 4.3)). (l – длина перпендикуляра, опущенного из точки О на направление действия силы (см. рис. 4.3)).
Направление вектора 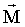 совпадает с направлением поступательного движения правого винта при его кратчайшем повороте от совпадает с направлением поступательного движения правого винта при его кратчайшем повороте от 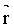 и и 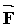 . .
Моментом силы относительно неподвижной оси z называется скалярная величина 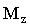 , равная проекции на эту ось вектора , равная проекции на эту ось вектора 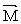 момента силы , определенного относительно произвольной точки О данной оси z. момента силы , определенного относительно произвольной точки О данной оси z.
Работа при вращении тела вокруг неподвижной оси z равна произведению момента 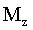 действующей силы относительно данной оси на угол поворота действующей силы относительно данной оси на угол поворота 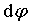 : :
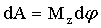 . .
Работа при вращении тела идет на увеличение его кинетической энергии:
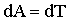 , но , но 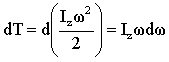 , ,
поэтому
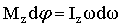 или или 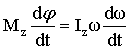 . .
Учитывая, что 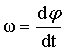 , получаем , получаем
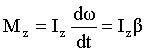 . (4.1) . (4.1)
Уравнение (4.1) представляет собой основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси z.
Можно показать, что если ось z совпадает с главной осью инерции (смотри раздел 4.5), проходящей через центр масс, то имеет место векторное равенство
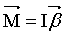 , ,
где 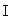 - главный момент инерции тела (момент инерции относительно главной оси). Таким образом, направление - главный момент инерции тела (момент инерции относительно главной оси). Таким образом, направление 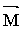 совпадает с направлением совпадает с направлением 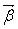 . .
4.4. Момент импульса и закон его сохранения
Моментом импульса 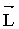 материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора 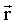 этой материальной точки, проведенного из точки О, на величину ее импульса этой материальной точки, проведенного из точки О, на величину ее импульса 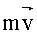 : :
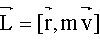 , ,
где 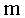 - масса материальной точки; - масса материальной точки; 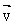 – ее скорость при поступательном движении или линейная скорость ее при вращательном движении. – ее скорость при поступательном движении или линейная скорость ее при вращательном движении.
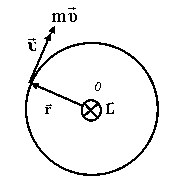
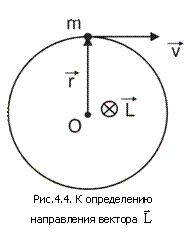 Вектор Вектор 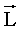 направлен так же, как и вектор угловой скорости направлен так же, как и вектор угловой скорости 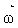 , т.е. вдоль оси вращения, согласно правилу правого винта (рис. 4.4). , т.е. вдоль оси вращения, согласно правилу правого винта (рис. 4.4).
Если твердое тело, вращающееся вокруг некоторой неподвижной оси z, представить в виде совокупности элементарных масс, и спроектировать моменты импульсов всех этих элементарных масс на это направление, получим момент импульса тела 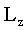 относительно этой оси ( относительно этой оси (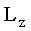 – скалярная величина). – скалярная величина).
Суммирование производим по всем элементарным массам 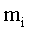 (имеющим линейную скорость (имеющим линейную скорость 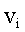 и радиус вращения и радиус вращения 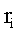 ), на которые разбивается тело. Так как ), на которые разбивается тело. Так как 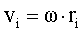 , где ω - угловая скорость вращения тела, а , где ω - угловая скорость вращения тела, а 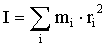 - момент инерции тела относительно данной оси, тогда момент импульса тела относительно оси z равен - момент инерции тела относительно данной оси, тогда момент импульса тела относительно оси z равен
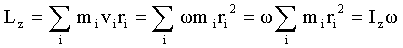 , ,
т.е.
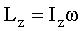 . (4.2) . (4.2)
В случае тела, вращающегося вокруг оси симметрии, векторы
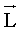 и и 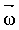 имеют одинаковое направление и тогда имеют одинаковое направление и тогда
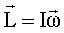 . .
Продифференцируем выражение (4.2) по времени:
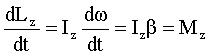 , ,
в итоге
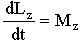 . (4.3) . (4.3)
Таким образом, производная по времени от момента импульса твердого тела относительно оси вращения равна моменту сил относительно той же оси.
Выражения (4.2) и (4.3) – еще две формы основного уравнения динамики вращательного движения твердого тела относительно неподвижной оси z.
Можно показать, что имеет место векторное равенство:
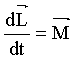 . (4.4) . (4.4)
Из уравнения (4.4) видно, что если момент внешних сил, действующих на тело, равен нулю, то момент импульса тела остается постоянным.
Если 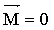 , то , то
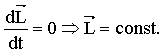 (4.5) (4.5)
Выражение (4.5) представляет собой закон сохранения момента импульса.
Для замкнутой системы тел закон сохранения момента импульса формулируется так: момент импульса замкнутой системы тел не меняется со временем, причем это утверждение справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Этот закон выполняется только в инерциальных системах отсчета.
Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его
изотропностью, т.е. с инвариантностью физических законов относительно поворота замкнутой системы в пространстве на любой угол.
4.5. Свободные оси. Гироскопы
Для того чтобы сохранить положение оси вращения твердого тела с течением времени неизменным, используют подшипники, в которых она удерживается. Но существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Эти оси называются свободными осями (или осями свободного вращения). Можно показать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями – они называются главными осями инерции тела.
Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней; главными осями инерции шара являются любые три взаимно перпендикулярные оси, проходящие через центр масс.
Свойство свободных осей сохранять свое положение в пространстве широко применяется в технике. Наиболее интересны в этом отношении гироскопы – массивные однородные тела, вращающиеся с большой угловой скоростью около своей оси симметрии, являющейся свободной осью. Гироскопы применяют в различных гироскопических навигационных приборах (гирокомпас, гирогоризонт и т.д.), а также в различных автопилотах.
4.6. Сопоставление формул кинематики и динамики
поступательного и вращательного движений
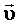 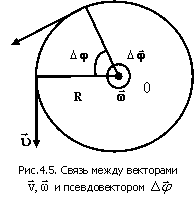 На рис.4.5 представлены направления векторов линейной На рис.4.5 представлены направления векторов линейной
скорости 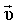 , угловой скорости , угловой скорости 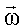 и псевдовектора угла поворота и псевдовектора угла поворота 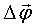 при вращательном движении. при вращательном движении.
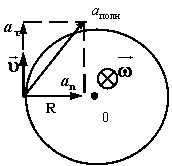
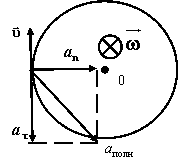
На рис.4.6 представлены направления векторов линейной
скорости 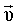 , тангенциального , тангенциального 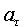 , нормального , нормального 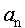 и полного и полного 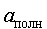 ускорений в случае равноускоренного (см. рис.4.6,а) и равнозамедленного (см. рис.4.6,б) вращательных движений. ускорений в случае равноускоренного (см. рис.4.6,а) и равнозамедленного (см. рис.4.6,б) вращательных движений.
 |
 |
| а) |
б) |
Рис.4.6. Связь между векторами 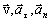 и и 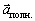
В табл.3 и 4 приведено сопоставление формул кинематики и динамики поступательного и вращательного движений.
Таблица 3
Сопоставление формул кинематики
поступательного и вращательного движений
|
Поступательное движение
|
Вращательное движение
|
|
перемещение
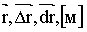
путь
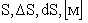
линейная скорость 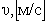
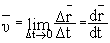
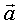 - ускорение - ускорение
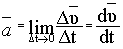 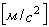
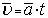
равноускоренное (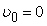 ) )
равнопеременное (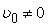 ) )
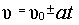
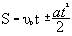 . .
|
угол поворота
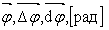
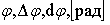
угловая скорость 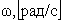
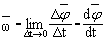
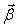 - угловое ускорение - угловое ускорение
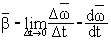 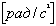
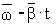
равноускоренное (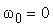 ) )
равнопеременное (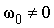 ) )
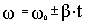
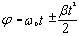
|
|
Связь линейной и угловой скорости
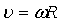 или или 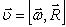
Связь тангенциального и углового ускорений
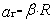
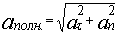 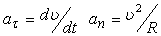
|
Таблица 4
Сопоставление формул кинематики
поступательного и вращательного движений
|
Поступательное движение
|
Вращательное движение
|
|
Инертные свойства - масса
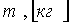
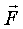 - сила - сила
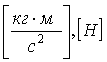
|
Инертные свойства – момент инерции
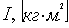
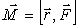 - момент силы, - момент силы, 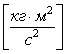 , ,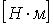
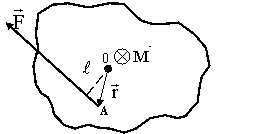
Момент силы направлен вдоль оси вращения по правилу правого винта (см . рис. ниже) . рис. ниже)
|
Продолжение табл.4
|
Поступательное движение
|
Вращательное движение
|
|
Основное уравнение динамики поступательного движения
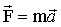 
Импульс - 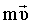
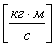 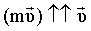
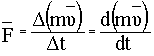
производная импульса определяет действующую силу
|
Основное уравнение динамики
вращательного движения
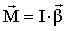 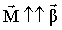
Момент импульса 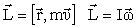
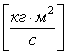 
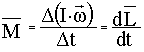 , т.е. , т.е.
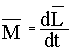 или или 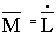
Уравнение моментов (производная момента импульса определяет вращающий момент силы)
|
Окончание табл.4
|
Поступательное движение
|
Вращательное движение
|
|
Кинетическая энергия при поступательном движении
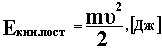
|
Кинетическая энергия
при вращательном движении
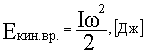

Плоское движение
(тело катится)
 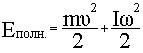 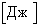
 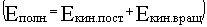
|
|
Работа при поступательном движении
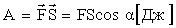
|
Работа при вращательном движении
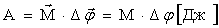
|
|
