|
2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
2.1. Первый закон Ньютона.
Инерциальные системы отсчета
Динамика – раздел механики, в котором изучаются законы движения тел и причины, вызывающие изменение характера их движения. В основе динамики лежат три закона, сформулированные в конце 17-го века И. Ньютоном. Эти законы не выводятся, а являются обобщением накопленного многовекового человеческого опыта. Их следует рассматривать в совокупности как систему взаимосвязанных законов, а не каждый закон в отдельности.
Первый закон утверждает, что существуют такие системы отсчета, в которых всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействия со стороны других тел не заставят его изменить это состояние.
Движение тел в отсутствие внешних воздействий называется движением по инерции, при этом проявляется особое динамическое свойство тел – инертность. Соответственно, первый закон Ньютона называют законом инерции, а системы отсчета, в которых он выполняется, называют инерциальными системами отсчета (ИСО). Все системы отсчета, которые можно считать инерциальными, должны двигаться друг относительно друга равномерно и прямолинейно.
В настоящее время экспериментально с большой точностью установлено, что практически идеально инерциальной является гелиоцентрическая система отсчета, начало координат которой находится в центре инерции (см. далее) Солнечной системы (приближенно – в центре Солнца), а оси координат проведены взаимно перпендикулярно в направлении трех удаленных звезд.
Для ИСО в рамках классической механики (т.е. для макроскопических тел, движущихся со скоростями, значительно меньшими скорости света) справедлив принцип относительности Галилея, согласно которому все ИСО по своим механическим свойствам эквивалентны друг другу. Это значит, что во всех ИСО одинаковы свойства пространства (однородность и изотропность) и времени (однородность), а также одинаково выполняются все законы механики.
Непосредственно из принципа относительности вытекают так называемые преобразования Галилея для координат и скоростей при переходе от одной ИСО к другой. Пусть инерциальная система K' движется с постоянной скоростью 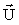 (она называется переносной) относительно другой инерциальной системы K (рис. 2.1). Для упрощения выберем оси координат X’, Y’, Z’ системы K’ параллельно соответствующим осям X, Y, Z системы K, причем так, чтобы оси Х и Х' совпадали друг с другом и были направлены вдоль вектора (она называется переносной) относительно другой инерциальной системы K (рис. 2.1). Для упрощения выберем оси координат X’, Y’, Z’ системы K’ параллельно соответствующим осям X, Y, Z системы K, причем так, чтобы оси Х и Х' совпадали друг с другом и были направлены вдоль вектора 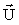 . Очевидно, если взять за начало отсчета времени момент, когда начала координат О и О' совпадали, то связь между радиусами-векторами . Очевидно, если взять за начало отсчета времени момент, когда начала координат О и О' совпадали, то связь между радиусами-векторами 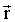 и и 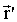 одной и той же точки А в K- и K’- cистемах может быть записана: одной и той же точки А в K- и K’- cистемах может быть записана:
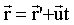 (2.1) (2.1)
и, кроме того,
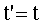 . .
При этом подразумевается абсолютность пространства и времени, т.е. одинаковость длин отрезков и хода времени во всех ИСО. Продифференцировав (2.1) по времени, найдем классический закон преобразования скорости:
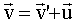 . (2.2) . (2.2)
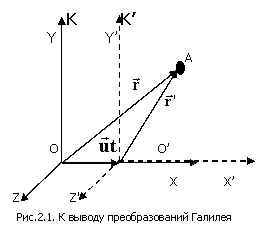
Дифференцируя это выражение по времени с учетом постоянства скорости 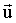 , получим , получим 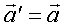 , т.е. ускорение материальной точки одинаково во всех ИСО. , т.е. ускорение материальной точки одинаково во всех ИСО.
2.2. Сила и масса. Второй и третий законы Ньютона
Как показывает опыт, в ИСО всякое тело получает ускорение либо деформируется только в результате действия на него других тел. В то же время действие одного тела на другое не бывает односторонним – всегда имеет место и обратное действие. Поэтому действия тел друг на друга носят характер взаимодействия. Количественной характеристикой взаимодействия тел служит векторная физическая величина, называемая силой 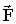 . Сила считается полностью определенной, если заданы ее модуль, направление в пространстве и точка приложения. Поскольку сила является причиной ускорения, принято считать, что . Сила считается полностью определенной, если заданы ее модуль, направление в пространстве и точка приложения. Поскольку сила является причиной ускорения, принято считать, что  . .
Опыт показывает, что ускорения, приобретаемые одним и тем же телом под действием разных сил, пропорциональны этим силам, следовательно, при любой по величине и направлению силе отношение 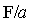 для данного тела остается постоянным. Для разных же тел это отношение различно. Таким образом, отношение для данного тела остается постоянным. Для разных же тел это отношение различно. Таким образом, отношение 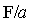 характеризует свойство тел препятствовать изменению их скорости, которое в разд. 2.1 было названо инертностью. В качестве количественной меры инертности тел вводится скалярная физическая величина, называемая массой m. В рамках классической механики масса обладает двумя важнейшими свойствами: характеризует свойство тел препятствовать изменению их скорости, которое в разд. 2.1 было названо инертностью. В качестве количественной меры инертности тел вводится скалярная физическая величина, называемая массой m. В рамках классической механики масса обладает двумя важнейшими свойствами:
1) аддитивностью, т.е. масса составного тела равна сумме масс его частей;
2) постоянством, т.е. масса не изменяется при движении тела.
Второй закон Ньютона: Ускорение материальной точки в инерциальной системе отсчета прямопропорционально действующей на него силе и обратно пропорционально ее массе. Математическая запись этого закона при надлежащем выборе единиц измерения величин имеет вид:
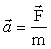 . .
Если на материальную точку одновременно действуют несколько сил 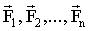 , то полное ускорение , то полное ускорение 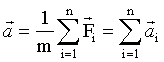 , где , где 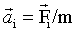 . Таким образом, каждая из сил, одновременно действующих на материальную точку, сообщает ей такое же ускорение, как если бы других сил не было. Это утверждение выражает принцип независимости действия сил. . Таким образом, каждая из сил, одновременно действующих на материальную точку, сообщает ей такое же ускорение, как если бы других сил не было. Это утверждение выражает принцип независимости действия сил.
Уравнение второго закона Ньютона при решении практических задач удобнее записывать
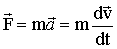 . .
Это основное уравнение динамики материальной точки. Учитывая постоянство массы в классической механике, можно внести ее под знак производной:
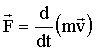 . (2.3) . (2.3)
Векторная величина в скобках 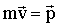 называется импульсом материальной точки. Подставив эту величину в (2.3), получим более общую запись второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе называется импульсом материальной точки. Подставив эту величину в (2.3), получим более общую запись второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе
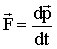 . (2.4) . (2.4)
Выражение (2.4) можно преобразовать к виду
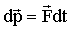 . .
Здесь векторная величина, записанная в правой части, называется элементарным импульсом силы 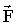 за бесконечно малое время за бесконечно малое время 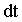 её действия. Это ещё один вариант записи второго закона Ньютона, который может быть сформулирован: изменение импульса материальной точки равно импульсу действующей на неё силы. её действия. Это ещё один вариант записи второго закона Ньютона, который может быть сформулирован: изменение импульса материальной точки равно импульсу действующей на неё силы.
Единицей силы в СИ является ньютон (Н): 1 Н – сила, которая массе 1 кг сообщает ускорение 1 м/с2 в направлении действия силы:
1 Н = 1 кг·м/с2 .
Третий закон Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия. Две материальные точки действуют друг на друга с силами, равными по величине и направленными в противоположные стороны вдоль прямой, соединяющей эти точки:
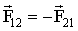 , ,
где 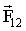 - сила, действующая на первую материальную точку со стороны второй; - сила, действующая на первую материальную точку со стороны второй; 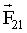 - сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам, всегда действуют попарно и являются силами одной природы. - сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам, всегда действуют попарно и являются силами одной природы.
Третий закон Ньютона существенно дополняет первый и второй законы. Значимость его в том, что он позволяет перейти от динамики отдельной материальной точки к динамике системы материальных точек.
2.3. Закон сохранения импульса. Центр масс системы
Механической системой называется совокупность материальных точек (тел), рассматриваемых как единое целое. Силы взаимодействия между материальными точками системы называются внутренними. Силы, с которыми внешние тела действуют на материальные точки системы, называются внешними. Механическая система, на которую не действуют внешние силы, называется замкнутой (или изолированной).
Из третьего закона Ньютона следует, что в любой механической системе геометрическая сумма всех внутренних сил равна нулю:
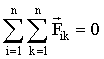 , ,
где n – число материальных точек в системе, а 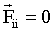 . .
Центром масс (или центром инерции) системы материальных точек называется точка С, радиус-вектор которой равен
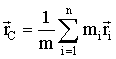 , (2.5) , (2.5)
где 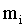 и и 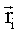 – масса и радиус-вектор i-й материальной точки, а – масса и радиус-вектор i-й материальной точки, а 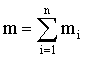 – масса всей системы. – масса всей системы.
Скорость центра масс определяется как производная радиуса-вектора (2.5)
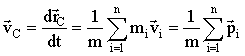 . (2.6) . (2.6)
Геометрическая сумма импульсов всех материальных точек системы в правой части выражения (2.6) называется импульсом системы 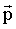 . Очевидно, что . Очевидно, что 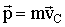 . Из второго и третьего законов Ньютона следует, что первая производная импульса системы по времени равна главному вектору всех внешних сил, приложенных к системе, . Из второго и третьего законов Ньютона следует, что первая производная импульса системы по времени равна главному вектору всех внешних сил, приложенных к системе,
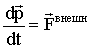 . .
Это уравнение выражает закон изменения импульса системы. На основании его можно сформулировать закон движения центра масс механической системы:
Центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе.
Математическая запись этого закона имеет вид
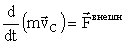 , или , или 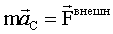 , ,
где 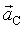 – ускорение центра масс. – ускорение центра масс.
Если механическая система является замкнутой, т.е. главный вектор внешних сил равен нулю, то, очевидно,
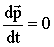 или или 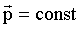 . .
Это и есть закон сохранения импульса замкнутой системы, являющийся одним из фундаментальных законов физики.
2.4. Силы в механике
2.4.1. Закон всемирного тяготения. Сила тяжести
Исаак Ньютон на основании законов Кеплера и основных законов динамики открыл всеобщий закон всемирного тяготения: между любыми материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек (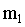 и и 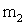 ) и обратно пропорциональная квадрату расстояния между ними ( ) и обратно пропорциональная квадрату расстояния между ними (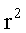 ): ):
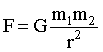 . .
Коэффициент пропорциональности 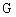 называется гравитационной постоянной, называется гравитационной постоянной, 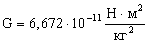 . Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. Ввиду малой величины . Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. Ввиду малой величины 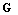 сила гравитационного взаимодействия может быть значительной только в случае больших масс. сила гравитационного взаимодействия может быть значительной только в случае больших масс.
Под действием силы притяжения к Земле все тела падают с одинаковым относительно поверхности Земли ускорением 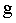 , которое называют ускорением свободного падения. Поэтому в системе отсчета, связанной с Землей, на всякое тело массой , которое называют ускорением свободного падения. Поэтому в системе отсчета, связанной с Землей, на всякое тело массой 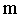 действует сила действует сила
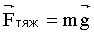 , ,
называемая силой тяжести.
Ускорение свободного падения изменяется вблизи поверхности Земли с широтой в пределах от 9,780 м/с2 на экваторе до 9,832 м/с2 на полюсах. Это обусловлено суточным вращением Земли и ее сплюснутостью у полюсов. Для решения практических задач используется значение 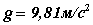 . .
Сила тяжести приближенно равна силе гравитационного притяжения тела к Земле (различие не превышает 0,36 % и обусловлено тем, что система отсчета, связанная с Землей, из-за её вращения не вполне инерциальная). Для тела на поверхности Земли
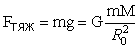 , ,
где 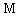 – масса Земли, – масса Земли, 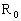 - радиус Земли. - радиус Земли.
Для тела, расположенного на высоте 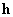 от поверхности Земли, от поверхности Земли,
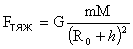 . .
Если подвесить тело (рис.2.2,а) или положить на опору
(рис.2.2,б), оно будет покоиться относительно Земли; при этом сила тяжести уравновешивается силой реакции подвеса или опоры (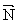 ). По третьему закону Ньютона тело действует на подвес или опору с силой ). По третьему закону Ньютона тело действует на подвес или опору с силой 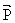 , которую называют весом тела. , которую называют весом тела.
Вес тела 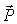 – это сила, с которой тело действует на вертикальный подвес или горизонтальную опору вследствие гравитационного притяжения к Земле. – это сила, с которой тело действует на вертикальный подвес или горизонтальную опору вследствие гравитационного притяжения к Земле.

а) б)
Рис.2.2. К определению понятия веса тела
В отсутствие вертикального ускорения силы 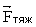 и и 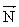 уравновешивают друг друга и уравновешивают друг друга и 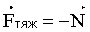 . Но по третьему закону Ньютона . Но по третьему закону Ньютона 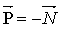 . Следовательно, . Следовательно,
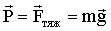 . .
Однако вес равен 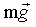 только в том случае, если тело и опора (подвес) неподвижны относительно Земли. Если опора (подвес) движется вместе с телом с ускорением только в том случае, если тело и опора (подвес) неподвижны относительно Земли. Если опора (подвес) движется вместе с телом с ускорением 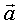 , вес тела равен , вес тела равен
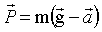 . .
2.4.2. Силы трения
Трение играет большую роль в природе и технике. Различают внешнее (сухое) и внутреннее (вязкое) трение.
 Внешним трением называется трение, возникающее между соприкасающимися поверхностями тел при их относительном перемещении. Если вдоль границы соприкасающихся тел хотя бы к одному из них приложена внешняя сила, но при этом тела неподвижны друг относительно друга, то говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трении скольжения или качения. Внешним трением называется трение, возникающее между соприкасающимися поверхностями тел при их относительном перемещении. Если вдоль границы соприкасающихся тел хотя бы к одному из них приложена внешняя сила, но при этом тела неподвижны друг относительно друга, то говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трении скольжения или качения.
Внутренним трением называют трение между частями одного и того же тела (например, между слоями жидкости или газа, движущимися с разными скоростями).
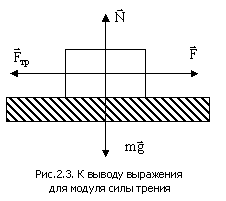
Рассмотрим закономерности сухого трения на примере тела, лежащего на плоскости, к которому приложена горизонтальная сила 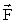 (рис.2.3). Тело придет в движение лишь тогда, когда сила (рис.2.3). Тело придет в движение лишь тогда, когда сила 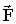 будет больше силы трения покоя. будет больше силы трения покоя.
Сила трения скольжения 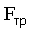 , а также максимальная сила трения покоя по модулю пропорциональны силе , а также максимальная сила трения покоя по модулю пропорциональны силе 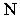 нормального давления, прижимающей трущиеся поверхности друг к другу нормального давления, прижимающей трущиеся поверхности друг к другу
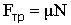 , ,
где 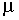 – коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей. – коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.
Если приложенная сила 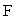 не превышает максимального значения силы трения покоя, то тело не придет в движение. не превышает максимального значения силы трения покоя, то тело не придет в движение.
Для тела, движущегося вдоль наклонной плоскости (рис.2.4), коэффициент трения равен тангенсу угла наклона 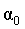 , при котором начинается скольжение тела по данной плоскости , при котором начинается скольжение тела по данной плоскости
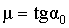 . .
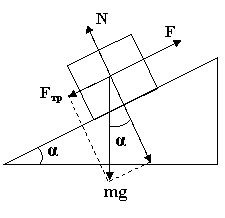
Рис.2.4. Тело на наклонной плоскости
Уменьшить силу трения можно, например, нанося на трущиеся поверхности смазку, заполняющую неровности между поверхностями, или заменив трение скольжения трением качения. Как показывают опыты, сила трения качения пропорциональна силе нормального давления и обратно пропорциональна радиусу катящегося тела (например, колеса, цилиндра или шара):
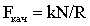 . .
2.4.3. Силы упругости
Все тела под действием приложенных к ним сил деформируются, т.е. изменяют свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой (упругие деформации наблюдаются, если деформирующая сила не превосходит предел упругости). Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются пластическими (или остаточными).
Рассмотрим пружину длиной 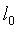 , один конец которой закреплен неподвижно, а к другому приложена внешняя сила , один конец которой закреплен неподвижно, а к другому приложена внешняя сила 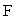 (рис. 2.5). Согласно закону Гука, сила упругости, возникающая в пружине, прямо пропорциональна удлинению пружины (рис. 2.5). Согласно закону Гука, сила упругости, возникающая в пружине, прямо пропорциональна удлинению пружины
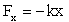 , ,
где 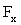 - проекция силы упругости на ось - проекция силы упругости на ось 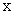 ; ; 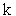 - жесткость пружины; - жесткость пружины; 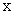 - удлинение пружины. - удлинение пружины.
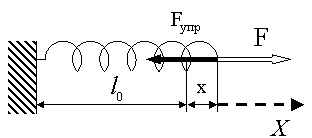
Рис.2.5. К закону Гука
Однородные стержни ведут себя при растяжении или одностороннем сжатии подобно пружине. Если к концам стержня длиной 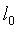 и площадью поперечного сечения и площадью поперечного сечения 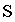 приложить направленные вдоль его оси силы приложить направленные вдоль его оси силы 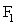 и и 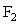 ( (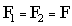 ), то длина стержня увеличится (при растяжении) или уменьшится (при сжатии) на ), то длина стержня увеличится (при растяжении) или уменьшится (при сжатии) на  (рис.2.6). (рис.2.6).
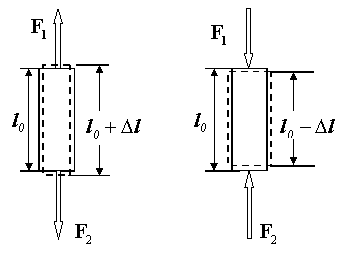
Рис.2.6. Деформации растяжения-сжатия в упругом стержне
Количественной мерой деформации стержня является относительная деформация
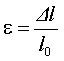 . .
Сила, действующая на единицу площади поперечного сечения, называется напряжением:
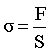 . .
Если сила направлена по нормали к поверхности, напряжение называется нормальным, если же по касательной – тангенциальным.
Экспериментально установлено, что относительное удлинение 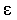 и напряжение и напряжение 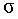 прямо пропорциональны друг другу: прямо пропорциональны друг другу:
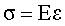 , ,
где коэффициент пропорциональности 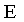 называется модулем Юнга. Измеряется эта величина в паскалях (1 Па=1 Н/м2). Модуль Юнга равен такому нормальному напряжению, при котором относительное удлинение было бы равно единице. называется модулем Юнга. Измеряется эта величина в паскалях (1 Па=1 Н/м2). Модуль Юнга равен такому нормальному напряжению, при котором относительное удлинение было бы равно единице.
|
