|
1. КИНЕМАТИКА
1.1. Основные понятия кинематики
Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.
Кинематика изучает движение тел без рассмотрения причин, обусловливающих это движение.
При описании механического движения используют физические модели материальной точки и абсолютно твердого тела.
Материальная точка – тело, размерами и формой которого можно пренебречь в условиях решаемой задачи. Очевидно, что одно и то же тело в одних условиях можно рассматривать как материальную точку, а в других – только как протяженное тело. Абсолютно твердое тело (часто называют просто твердое тело) – система материальных точек, расстояние между которыми не меняется в процессе движения.
Различные сложные случаи движения твердого тела можно представить как последовательную комбинацию двух основных видов движения:
а) поступательное движение – движение, при котором прямая, проходящая через две произвольные точки твердого тела, всегда остается параллельной своему первоначальному положению;
б) вращательное движение – движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения, а сами окружности лежат в параллельных плоскостях.
Определить положение тела в пространстве, а также изменение этого положения возможно только по отношению к другим телам. Обычно в системе тел выбирают одно, которое служит телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов образует систему отсчета (СО). Это понятие является фундаментальным в физике, поскольку пространственно-временное описание движения не имеет смысла, пока не определена СО. Тело отсчета обычно совмещают с началом координат.
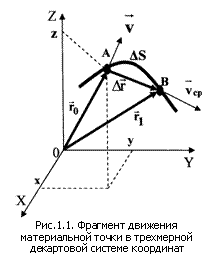 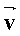  На рис.1.1 показан фрагмент движения материальной точки в трехмерной декартовой системе координат (XYZ) из начального положения – (·) А в конечное положение – (·) В. Эти геометрические точки характеризуются соответственно радиусами-векторами На рис.1.1 показан фрагмент движения материальной точки в трехмерной декартовой системе координат (XYZ) из начального положения – (·) А в конечное положение – (·) В. Эти геометрические точки характеризуются соответственно радиусами-векторами 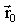 и и 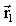 – векторами, проведенными из начала координат в указанные точки. Радиус-вектор любой точки может быть выражен через её координаты (x,y.z): – векторами, проведенными из начала координат в указанные точки. Радиус-вектор любой точки может быть выражен через её координаты (x,y.z):
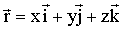 . .
Здесь 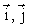 и и 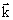 – единичные векторы (орты), направленные вдоль координатных осей OX, OY и OZ. Не трудно видеть, что – единичные векторы (орты), направленные вдоль координатных осей OX, OY и OZ. Не трудно видеть, что 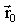 и и 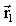 связаны между собой соотношением связаны между собой соотношением
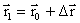 , ,
где 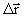 - вектор, называемый перемещением. Модуль перемещения равен кратчайшему расстоянию между А и В. Совокупность точек пространства, через которые тело последовательно проходит во время своего движения, называется траекторией. В общем случае это может быть любая трехмерная кривая. В дальнейшем для простоты мы будем в основном рассматривать так называемое плоское движение, при котором траектория лежит в одной определенной плоскости. Длина участка траектории между точками А и В называется путь и обычно обозначается S или ΔS. - вектор, называемый перемещением. Модуль перемещения равен кратчайшему расстоянию между А и В. Совокупность точек пространства, через которые тело последовательно проходит во время своего движения, называется траекторией. В общем случае это может быть любая трехмерная кривая. В дальнейшем для простоты мы будем в основном рассматривать так называемое плоское движение, при котором траектория лежит в одной определенной плоскости. Длина участка траектории между точками А и В называется путь и обычно обозначается S или ΔS.
1.2. Скорость
Скорость – это векторная физическая величина, характеризующая быстроту перемещения тела в пространстве. Отношение вектора перемещения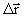 к отрезку времени Δt, в течение которого это перемещение произошло, называют средней скоростью: к отрезку времени Δt, в течение которого это перемещение произошло, называют средней скоростью:
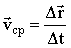 . .
Переходя к пределу этого отношения, получим мгновенную скорость:
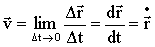 . . 
Таким образом, мгновенная скорость – векторная величина, определяемая как производная радиуса-вектора движущейся материальной точки по времени. Вектор мгновенной скорости направлен по касательной к траектории в сторону движения. Как и радиус-вектор, вектор скорости может быть разложен на составляющие по осям OX, OY и OZ:
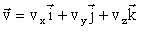 , ,
где 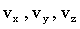 – проекции вектора скорости на соответствующие оси. При этом они являются производными координат по времени: – проекции вектора скорости на соответствующие оси. При этом они являются производными координат по времени:
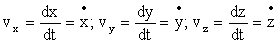 . .
Модуль вектора скорости точки:
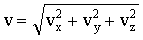 . .
При решении многих практических задач используется также средняя путевая скорость – скалярная величина, равная отношению пройденного пути 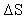 к интервалу времени к интервалу времени 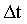 , затраченного на его прохождение: , затраченного на его прохождение:
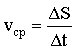 . .
Переходя к пределу при 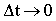 и учитывая, что при этом элементарный путь и учитывая, что при этом элементарный путь 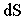 бесконечно близок к модулю элементарного перемещения бесконечно близок к модулю элементарного перемещения 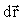 , получаем, что модуль мгновенной скорости равен первой производной пути по времени , получаем, что модуль мгновенной скорости равен первой производной пути по времени
 . .
Если известен вид зависимости 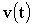 , то путь, пройденный точкой за промежуток времени от t1 до t2, может быть найден путем интегрирования , то путь, пройденный точкой за промежуток времени от t1 до t2, может быть найден путем интегрирования
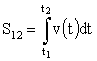 . .
 Как известно из математического анализа, определенный интеграл численно равен площади фигуры, заключенной между графиком функции и осью аргумента. Поэтому, если задан график скорости, с его помощью может быть численно найден путь за интересующий нас отрезок времени (рис.1.2). Как известно из математического анализа, определенный интеграл численно равен площади фигуры, заключенной между графиком функции и осью аргумента. Поэтому, если задан график скорости, с его помощью может быть численно найден путь за интересующий нас отрезок времени (рис.1.2).
1.3. Неравномерное движение. Ускорение
Если скорость тела (материальной точки) с течением времени изменяется по величине или направлению, то такое движение называется неравномерным. Векторная физическая величина, определяющая быстроту изменения скорости по модулю и направлению, называется ускорением. Среднее ускорение за промежуток времени Δt:
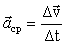 , (1.1) , (1.1)
где 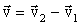 - изменение вектора скорости за время Δt. - изменение вектора скорости за время Δt.
Переходя к пределу в формуле (1.1), получаем выражение для мгновенного ускорения:
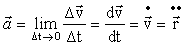 . .
Вектор ускорения может быть выражен следующими способами:
· в виде суммы составляющих по осям координат
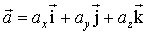 , ,
где 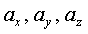 − проекции вектора ускорения на соответствующие оси; − проекции вектора ускорения на соответствующие оси;
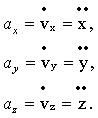
· в виде суммы взаимно перпендикулярных векторов тангенциального (касательного) и нормального ускорений (здесь мы ограничиваемся случаем плоского движения, при котором все точки траектории лежат в одной плоскости – (рис.1.3)
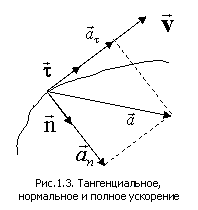 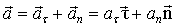 , ,
где 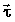 – единичный вектор, сонаправленный с вектором скорости, т.е. по касательной к траектории; – единичный вектор, сонаправленный с вектором скорости, т.е. по касательной к траектории; 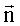 – единичный вектор, направленный к центру кривизны траектории, т.е. перпендикулярно к – единичный вектор, направленный к центру кривизны траектории, т.е. перпендикулярно к 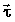 . Тангенциальное ускорение характеризует быстроту изменения модуля скорости: . Тангенциальное ускорение характеризует быстроту изменения модуля скорости:
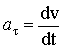 . (1.2) . (1.2)
Нормальное ускорение характеризует быстроту изменения скорости по направлению. Его модуль:
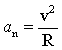 , (1.3) , (1.3)
где R – радиус кривизны траектории в данной точке. Модуль полного ускорения равен
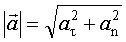 . (1.4) . (1.4)
Разным сочетаниям тангенциального и нормального ускорений соответствуют различные виды плоского движения, приведенные в табл.1.
Таблица 1
Виды плоского движения
|
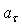
|
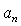
|
Вид движения
|
|
0
|
0
|
Прямолинейное равномерное
|
|
const
|
0
|
Прямолинейное равнопеременное
|
|
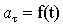
|
0
|
Прямолинейное неравномерное
|
|
0
|
const
|
Равномерное по окружности
|
|
0
|
≠ 0
|
Криволинейное равномерное
|
|
const
|
≠ 0
|
Криволинейное равнопеременное
|
|
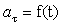
|
≠ 0
|
Криволинейное неравномерное
|
1.4. Кинематические уравнения
Кинематические уравнения – это уравнения, показывающие зависимость основных кинематических характеристик (радиуса-вектора, координат, скорости, ускорения) от времени. В случае произвольного движения эти уравнения могут быть весьма сложными. Ниже приведены кинематические уравнения для некоторых простых случаев.
1.4.1. Равномерное прямолинейное движение
Это такое движение, при котором материальная точка (тело) за любые равные промежутки времени проходит одинаковые отрезки по прямой. Уравнение скорости для такого движения имеет вид:
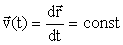 . (1.5) . (1.5)
Выразим отсюда элементарное перемещение 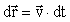 и, проинтегрировав по времени в пределах (0, t), получим уравнение радиуса-вектора и, проинтегрировав по времени в пределах (0, t), получим уравнение радиуса-вектора
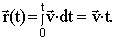
Полагая для простоты, что вектор скорости направлен вдоль оси ОХ, можно записать уравнение (1.5) в скалярной форме:
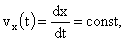 (1.5,а) (1.5,а)
откуда
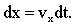 (1.5.б) (1.5.б)
Интегрируя выражение (1.5,б) по времени в пределах (0, t), получим уравнение пути:
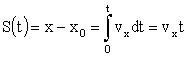 . .
Здесь х0 – начальная координата движущейся точки. Отсюда уравнение координаты имеет вид:
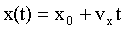 . .
Не следует забывать, что в зависимости от выбора положительного направления оси ОХ численное значение 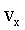 может быть как положительным, так и отрицательным. может быть как положительным, так и отрицательным.
1.4.2. Равнопеременное движение
Это такое движение, при котором материальная точка (тело) за любые равные промежутки времени изменяет свою скорость на одну и ту же величину, т.е. имеет постоянное ускорение 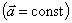 . При равнопеременном прямолинейном движении возможны два варианта: равноускоренное и равнозамедленное движение. . При равнопеременном прямолинейном движении возможны два варианта: равноускоренное и равнозамедленное движение.
Первый вариант соответствует ситуации, когда начальная скорость 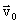 либо равна 0, либо сонаправлена с ускорением либо равна 0, либо сонаправлена с ускорением 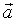 . Примером такого варианта движения является падение тела с некоторой высоты: либо свободно отпущенного, либо брошенного с начальной скоростью вертикально вниз. . Примером такого варианта движения является падение тела с некоторой высоты: либо свободно отпущенного, либо брошенного с начальной скоростью вертикально вниз.
Второй вариант соответствует ситуации, когда 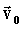 направлена противоположно направлена противоположно 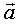 . Например, движение тела, брошенного вертикально вверх (на участке траектории до верхней точки подъема). . Например, движение тела, брошенного вертикально вверх (на участке траектории до верхней точки подъема).
Уравнение ускорения для прямолинейного вдоль оси ОХ равнопеременного движения в скалярной записи имеет вид:
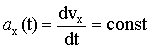 . (1.6) . (1.6)
Элементарное изменение скорости выразится 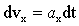 , откуда интегрированием получаем приращение скорости за конечный промежуток времени (0, t) , откуда интегрированием получаем приращение скорости за конечный промежуток времени (0, t)
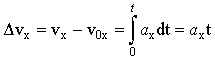 , ,
и, окончательно, уравнение скорости:
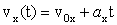 . (1.7) . (1.7)
Далее, подставляя (1.7) в (1.5,б) и интегрируя с учетом начальных условий, получим уравнение координаты:
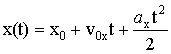 . (1.8) . (1.8)
1.5. Кинематика вращательного движения
При описании вращательного движения твердого тела относительно неподвижной в данной системе отсчета принято использовать векторные величины особого рода. В отличие от рассмотренных выше полярных векторов 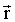 (радиус-вектор), (радиус-вектор), 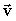 (скорость), (скорость), 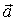 (ускорение), направление которых естественным образом вытекает из природы самих величин, направление векторов, характеризующих вращательное движение, совпадает с осью вращения, поэтому их называют аксиальными (лат. axis – ось). (ускорение), направление которых естественным образом вытекает из природы самих величин, направление векторов, характеризующих вращательное движение, совпадает с осью вращения, поэтому их называют аксиальными (лат. axis – ось).
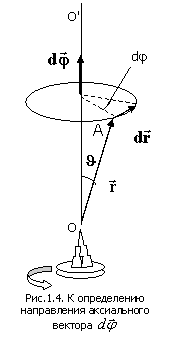 Элементарный поворот Элементарный поворот 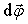 – аксиальный вектор, модуль которого равен углу поворота dφ, а направление вдоль оси вращения ОО' (см. рис. 1.4) определяется правилом правого винта. Линейное перемещение – аксиальный вектор, модуль которого равен углу поворота dφ, а направление вдоль оси вращения ОО' (см. рис. 1.4) определяется правилом правого винта. Линейное перемещение 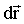 произвольной точки А твердого тела связано с радиусом-вектором произвольной точки А твердого тела связано с радиусом-вектором 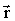 и поворотом и поворотом 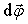 соотношением соотношением 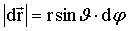 или в векторном виде через векторное произведение: или в векторном виде через векторное произведение:
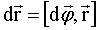 . (1.9) . (1.9)
Соотношение (1.9) справедливо именно для бесконечно малого поворота 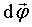 . .
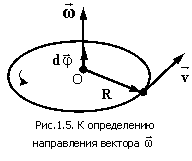 Угловая скорость Угловая скорость 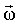 – аксиальный вектор, определяемый производной вектора поворота по времени – аксиальный вектор, определяемый производной вектора поворота по времени
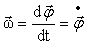 . .
Вектор 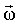 , как и вектор , как и вектор 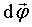 , направлен вдоль оси вращения по правилу правого винта (рис.1.5). , направлен вдоль оси вращения по правилу правого винта (рис.1.5).
Угловое ускорение 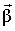 – аксиальный вектор, определяемый производной вектора угловой скорости по времени – аксиальный вектор, определяемый производной вектора угловой скорости по времени
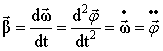 . .
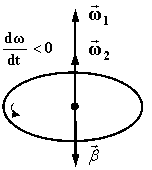
При ускоренном движении вектор 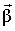 по направлению совпадает с по направлению совпадает с 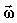 (рис. 1.6,а), а при замедленном - векторы (рис. 1.6,а), а при замедленном - векторы 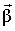 и и 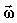 направлены противоположно друг другу (рис. 1.6,б). направлены противоположно друг другу (рис. 1.6,б).
а) б)
Рис.1.6. Связь между направлениями векторов 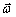 и и 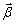
Важное замечание: решение всех задач на вращение твердого тела вокруг неподвижной оси по форме аналогично задачам на прямолинейное движение точки. Достаточно заменить линейные величины 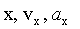 на соответствующие им угловые на соответствующие им угловые 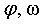 и и 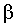 , и мы получим уравнения, аналогичные (1.6)-(1.8). , и мы получим уравнения, аналогичные (1.6)-(1.8).
1.6. Связь между линейными и угловыми величинами
Обратимся к рис. 1.4 и формуле (1.9). Для того чтобы связать линейную скорость 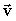 произвольной точки А твердого тела с угловой скоростью произвольной точки А твердого тела с угловой скоростью 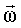 вращения этого тела вокруг неподвижной оси ОО’, поделим обе части формулы на вращения этого тела вокруг неподвижной оси ОО’, поделим обе части формулы на 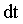 . Учитывая, что . Учитывая, что 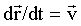 и и 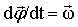 , получим , получим
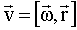 , (1.10) , (1.10)
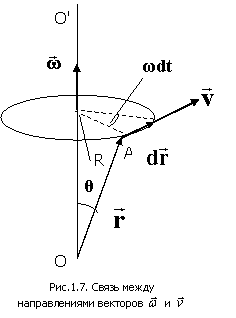 т.е. линейная скорость вращающейся точки равна векторному произведению угловой скорости на радиус-вектор этой точки (рис.1.7). Модуль вектора (1.10) равен т.е. линейная скорость вращающейся точки равна векторному произведению угловой скорости на радиус-вектор этой точки (рис.1.7). Модуль вектора (1.10) равен 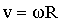 , где , где 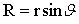 – радиус окружности, по которой движется точка А. Подставляя это выражение в формулы (1.2) и (1.3), получим – радиус окружности, по которой движется точка А. Подставляя это выражение в формулы (1.2) и (1.3), получим 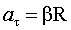 и и 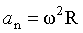 , откуда модуль полного ускорения согласно (1.4) равен , откуда модуль полного ускорения согласно (1.4) равен
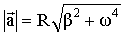 . .
|
