|
|
|
Сложение колебаний.
Векторная диаграмма
 Гармонические колебания удобно представлять в виде векторных
(круговых) диаграмм. В этом случае гармоническое колебание совершает проекция радиус-вектора, равного по модулю амплитуде колебаний
A. Воспользуемся методом векторных диаграмм при сложении гармонических колебаний одинакового направления с одинаковыми частотами.
Смещение x колеблющегося тела равно сумме смещений x1 и x2, которые записываются следующим образом: Гармонические колебания удобно представлять в виде векторных
(круговых) диаграмм. В этом случае гармоническое колебание совершает проекция радиус-вектора, равного по модулю амплитуде колебаний
A. Воспользуемся методом векторных диаграмм при сложении гармонических колебаний одинакового направления с одинаковыми частотами.
Смещение x колеблющегося тела равно сумме смещений x1 и x2, которые записываются следующим образом:
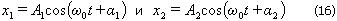
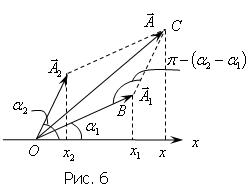
Представим оба колебания с помощью векторов 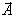 1 и 1 и 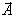 2
(рис. 6). Построим по правилам сложения векторов результирующий вектор 2
(рис. 6). Построим по правилам сложения векторов результирующий вектор 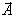 .
Легко видеть, что проекция этого вектора на ось x равна сумме проекций слагаемых векторов x= x1 + x2.
Следовательно, проекция вектора .
Легко видеть, что проекция этого вектора на ось x равна сумме проекций слагаемых векторов x= x1 + x2.
Следовательно, проекция вектора 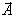 представляет собой результирующее колебание. представляет собой результирующее колебание.
Этот вектор вращается с той же угловой скоростью (циклической частотой) ω0, как и векторы
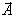 1 и 1 и 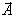 2, так что результирующее движение будет
гармоническим колебанием с частотой ω0, , амплитудой A и начальной фазой α. Из построения видно, что 2, так что результирующее движение будет
гармоническим колебанием с частотой ω0, , амплитудой A и начальной фазой α. Из построения видно, что
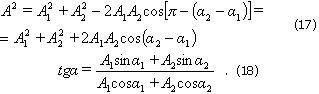
Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения вращающихся векторов.
Проанализируем выражение (17) для амплитуды:
а) если разность фаз колебаний α2 - α1 = 0 , т.е. колебания происходят в одинаковой фазе, то амплитуда результирующего колебания равна
A=A1+A2;
б) если разность фаз колебаний α2 - α1 =±Π, т.е. колебания находятся в противофазе, то амплитуда результирующего колебания
A=|A1-A2|.
Биения
Особый интерес представляет случай, когда два складываемых колебания одинакового направления мало отличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание называется биением.
Пусть частота одного колебания ω1=ω, а частота второго колебания ω2=ω+Δω,
причем Δω«ω. Амплитуды обоих колебаний полагаем одинаковыми и равными A. Для упрощения расчетов полагаем начальные фазы колебаний равными нулю. Тогда уравнения складываемых колебаний будут иметь следующий вид:
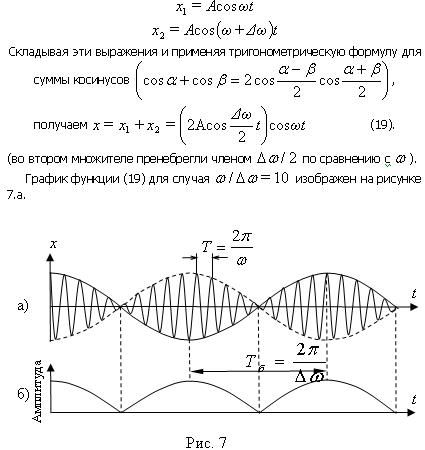
Заключенный в скобки множитель в формуле (19) изменяется гораздо медленнее, чем второй множитель, так как Δω«ω .
Это дает нам основание рассматривать колебание (19) как гармоническое колебание частоты ω, амплитуда которого изменяется по некоторому закону. Выражением этого закона не может быть множитель, стоящий в скобках, так как он изменяется от
2A до 2A, в то время, как амплитуда по определению – величина положительная. График амплитуды показан на рис 7.б. Аналитическое выражение амплитуды, очевидно, имеет вид:
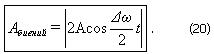
Функция (20) – периодическая функция с частотой в два раза превышающей частоту выражения, стоящего под знаком модуля, т.е. с частотой
Δω. Заменяя в выражении (19) амплитуду через значение (20), получаем уравнение биений:
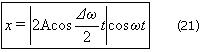
Сложение взаимно перпендикулярных колебаний
Допустим, что материальная точка (тело) может совершать колебания как вдоль оси X, так и вдоль перпендикулярной оси Y. Если возбудить оба колебания, материальная точка будет двигаться по некоторой криволинейной траектории, форма которой зависит от разности фаз колебаний. Выберем начало отсчета времени так, чтобы начальная фаза одного колебания была равна нулю. Тогда уравнения запишутся следующим образом:
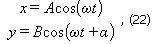
где α - разность фаз складываемых колебаний, A и B — амплитуды колебаний.
Выражения (22) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (22) параметр t. Из первого уравнения следует, что
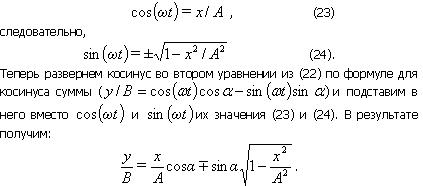
Перенесем все члены без корня в левую часть уравнения и возведем его в квадрат. После несложных преобразований получим уравнение эллипса, оси которого повернуты относительно координатных осей:

Ориентация эллипса и величина полуосей зависят довольно сложным образом от амплитуд A и B и разности фаз α.
Рассмотрим некоторые частные случаи.



происходит по медленно видоизменяющейся кривой, которая будет последовательно принимать форму, отвечающую всем значениям разности фаз от -Π до Π.
Если частоты взаимно перпендикулярных колебаний неодинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу.
На рис.11 показана одна из простейших траекторий, получающаяся при отношении частот 1:2 и разности фаз Π/2.Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу.
Фигуры Лиссажу позволяют найти частоту одного из колебаний, если известна частота другого. Это обусловлено тем, что кратность частот легко находится с помощью секущих, параллельных координатным осям.
|
|
|
