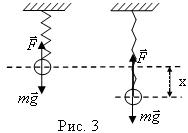
|
|
|
Пружинный маятник (рис. 3)
Применим к движению груза на пружине второй закон Ньютона:
Мы нашли собственную циклическую частоту (7) и период колебаний (8) груза на пружине.
Физический маятник (рис. 4)
Физическим маятником называется твердое тело, колеблющееся относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести. При небольших углах отклонения ( α-мал) физический маятник совершает гармонические колебания. Сила, возвращающая маятник в положение равновесия, представляет собой составляющую силы тяжести, приложенную в точке C :
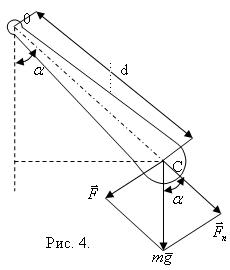
F=mgsinα
Момент этой силы относительно оси O равен: M= -Fl= mgdsinα , где l = dsinα - плечо силы F относительно оси O, знак минус соответствует тому, что момент M стремится вернуть маятник в положение равновесия, аналогично квазиупругой силе.
В соответствии с уравнением динамики вращательного движения
где d-расстояние от центра тяжести до оси вращения.
Если период колебаний не зависит от амплитуды, то такие колебания называются изохронными. Мы видим, что малые колебания физического маятника изохронны. Колебания приближенно изохронны, когда угловая амплитуда колебаний не превышает нескольких градусов. При больших амплитудах изохронность нарушается. На свойстве изохронности колебаний маятника основано его применение в часах.
Математический маятник (рис. 5)
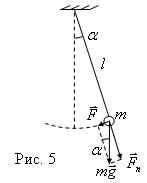 Математический маятник является частным случаем физического маятника. Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, к которой подвешена масса, сосредоточенная в одной точке. Примером математического маятника может служить шарик, подвешенный на длинной нити. В случае математического маятника d=l, I= ml2, где l-длина математического маятника. Тогда формулы (11) и (12) запишутся в виде:
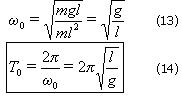
Сравнивая формулы (12) и (14), заключаем, что физический маятник колеблется с периодом математического маятника, длина которого
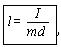
называется приведенной длиной физического маятника. |
|
|
