|
|
|
Упругие волны
Упругими (механическими) волнами называются механические возмущения, распространяющиеся в упругой среде.
Упругие волны бывают продольными (в которых частицы среды колеблются в направлении распространения волны) и поперечными (в которых частицы колеблются в плоскостях, перпендикулярных направлению распространения волны).
Внутри жидкостей и в газах возникают только продольные волны, в твёрдых телах – продольные и поперечные.
Длиной волны называется расстояние между ближайшими частицами, колеблющимися в одинаковой фазе
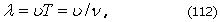
где - скорость волны, - период, - частота.
Уравнение бегущей волны
Бегущими называются волны, которые переносят в пространстве энергию.
Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением:
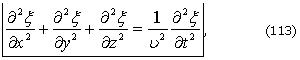
которое является дифференциальным уравнением в частных производных.
Здесь ξ(x,y,z,t) - смещение колеблющейся частицы, как функция координат и времени, ν - фазовая скорость, т.е. скорость перемещения фазы колебаний.
<>Для плоской волны волновое уравнение имеет вид:
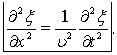
Решение этого уравнения является уравнением бегущей плоской волны, распространяющейся вдоль положительного направления оси в среде, не поглощающей энергию:
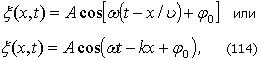
где A - амплитуда волны, ω - циклическая частота, 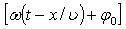 - фаза волны, φ0 - начальная фаза, - фаза волны, φ0 - начальная фаза, 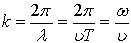 - волновое число, ν фазовая скорость. - волновое число, ν фазовая скорость.
Принцип суперпозиции. Интерференция волн
Принцип суперпозиции (наложения) волн: при распространении в среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы каждой волны.
Интерференция волн – наложение двух (или нескольких) когерентных волн, в результате чего происходит усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн.
Когерентными называются волны одного направления одинаковой частоты и постоянной разности фаз.
Рассмотрим наложение двух когерентных волн, возбуждаемых точечными источниками (для простоты начальные фазы φ0 = 0):
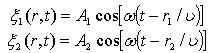
Разность фаз этих колебаний равна
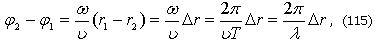
где 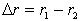 - разность хода волн, - разность хода волн, 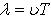 - длина волны. - длина волны.
1) если колебания происходят в одинаковой фазе, т.е.
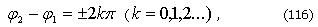
то наблюдается максимум интерференции. Приравниваем (115) и (116):
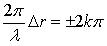
Получаем условие максимума при интерференции:
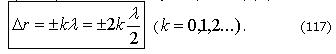
В этом случае A = A1 + A2.
2) если колебания происходят в противофазе, т.е.
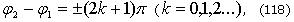
то наблюдается минимум интерференции. Приравниваем (115) и (117):
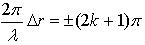
Получаем условие минимума при интерференции:
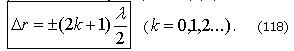
В этом случае A = |A1 + A2|.
|
|
|
