Вынужденные электрические колебания.
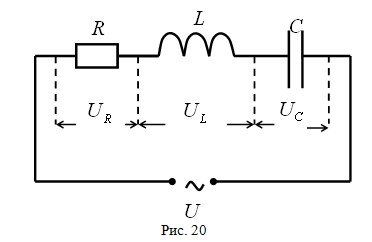
Чтобы вызвать вынужденные колебания, нужно оказать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний это можно осуществить, если включить последовательно с элементами контура переменную э.д.с. Или, разорвав контур, подать на образовавшиеся контакты переменное напряжение (рис. 20):
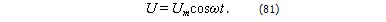
Это напряжение нужно прибавить к э.д.с. самоиндукции. В результате формула (69) примет вид
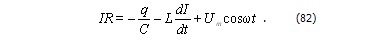
Произведя преобразования, получим уравнение
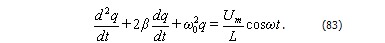
Частное решение уравнения (83) имеет вид
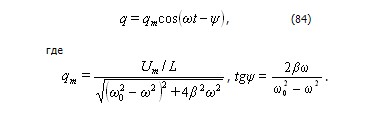
Подстановка значений и дает:
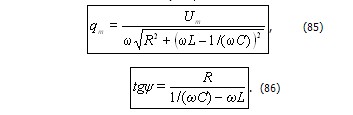
Общее решение получится, если к частному решению (84) прибавить решение соответствующего однородного уравнения (72), которое по прошествии достаточного времени становиться очень малым и им можно пренебречь. Следовательно, установившиеся вынужденные колебания описываются функцией (84).
Продифференцировав выражение (84) по времени, найдем силу тока в контуре при установившихся колебаниях:
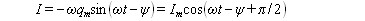
Запишем это выражение в виде
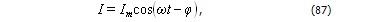
В соответствии с (86):
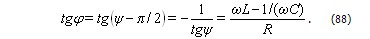
Из этой формулы следует, что ток отстаёт по фазе от напряжения cогласно (85)
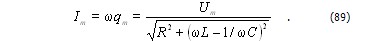
Представим соотношение (82) в виде
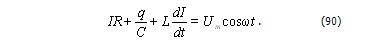
Произведение равно напряжению на активном сопротивлении. С учетом этого можно написать
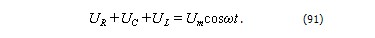
Таким образом, сумма напряжений на отдельных элементах контура равна в каждый момент времени напряжению, приложенному извне (см. рис.20).
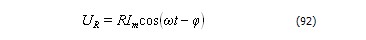
В соответствии с (87)
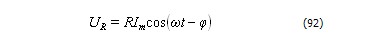
Разделив выражение (84) на электроёмкость, получим напряжение на конденсаторе
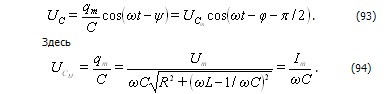
Умножив производную функции (87) на L, получим напряжение на индуктивности: (87)
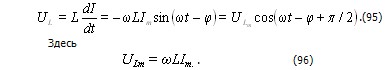
Сопоставление формул (87), (92), (93), (95) показывает, что напряжение на электроёмкости отстаёт по фазе от силы тока на . Напряжение на активном сопротивлении изменяется в фазе с током. Фазовые соотношения можно представить очень наглядно с помощью векторной диаграммы. Напомним, что гармоническое колебание (или гармоническую функцию) можно задать с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с некоторой осью угол, равный начальной фазе колебаний.
|
|
