Свободные электрические колебания в контуре без активного сопротивления.
При рассмотрении электрических колебаний приходится иметь дело с токами, изменяющимися со временем. Закон Ома и вытекающие из него правила Кирхгофа были установлены для постоянного тока. Однако они остаются справедливыми и для мгновенных значений изменяющихся тока и напряжения, если их изменения происходят не слишком быстро. Электромагнитные возмущения распространяются по цепи с огромной скоростью, равной скорости света.
Ток называется квазистационарным, когда мгновенные значения тока оказываются практически одинаковыми на всех участках цепи. Для периодически изменяющихся токов условие квазистационарности будет выполнено, если
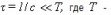 - период изменений.
Мы будем рассматривать только квазистационарные токи при изучении всех видов электрических колебаний. Мгновенные значения квазистационарных токов подчиняются закону Ома. Следовательно, для них справедливы и правила Кирхгофа.
В цепи, содержащей катушку индуктивностью и конденсатор ёмкостью , могут возникать электрические колебания. Поэтому такую цепь называют колебательным контуром. Выясним, каким образом в колебательном контуре возникают и поддерживаются электрические колебания.
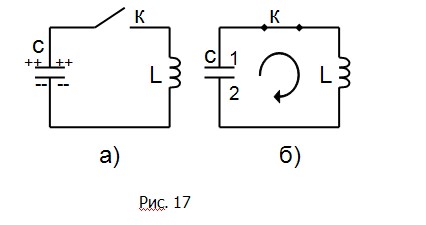
Пусть вначале верхняя обкладка конденсатора заряжена положительно, а нижняя отрицательно (рис. 17,а). При этом вся энергия колебательного контура сосредоточена в конденсаторе. Замкнем ключ K. Конденсатор начнет разряжаться, и через катушку L потечет ток. Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки. Этот процесс закончится, когда конденсатор полностью разрядиться, а ток в цепи достигнет максимума (рис.17,б). С этого момента ток, не меняя направления, начнет убывать. Однако он прекратится не сразу – его будет поддерживать э.д.с. самоиндукции. Ток будет перезаряжать конденсатор, возникает электрическое поле, стремящееся ослабить ток. Наконец ток прекратился, а заряд на конденсаторе достигнет максимума. С этого момента конденсатор начнет разряжаться опять, ток потечет в обратном направлении и т.д. - процесс будет повторяться.
В контуре при отсутствии сопротивления проводников совершаются строго периодические колебания. В ходе процесса периодически изменяются заряд на обкладках конденсатора, напряжение на нём и ток через катушку. Колебания сопровождаются взаимными превращениями энергии электрического и магнитного полей.
Найдем уравнение колебаний в контуре без активного сопротивления. Прежде всего, выберем положительное направление обхода контура, например, по часовой стрелке, т.е. условимся считать положительным ток, заряжающий конденсатор. Тогда
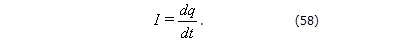
Напишем для колебательного контура выражение закона Ома:
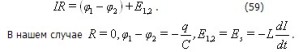
Подставив эти значения в (59), получаем:
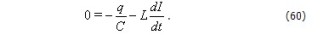
Учитывая,что 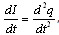 получаем уравнение 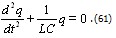
Сравнение уравнения (61) с уравнением (5) показывает, что уравнение (61) является дифференциальным уравнением гармонических колебаний. Из этого сравнения находим собственную частоту колебаний в контуре:
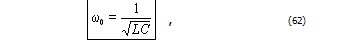
а уравнение (61) принимает вид:
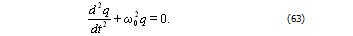
Решением этого уравнения является гармоническая функция
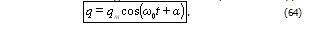
Для периода собственных колебаний получается так называемая формула Томсона:
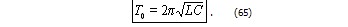
Напряжение на конденсаторе равно
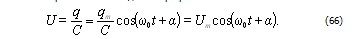
Продифференцировав функцию (64), получим выражение для силы тока:
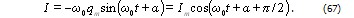
Таким образом, сила тока опережает по фазе напряжение на конденсаторе на 90.
Сопоставление формул (64) и (66) с формулой (67) показывает, что в момент, когда ток достигает наибольшего значения, заряд и напряжение на конденсаторе обращаются в нуль, и наоборот. Из формул (66) и (67) следует, что

|
|
