1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Уравнение гармонических колебаний
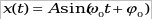 , ,
где X – смещение точки от положения равновесия, А – амплитуда колебаний,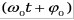 - фаза колебаний, w0– круговая (циклическая частота), t – время, - фаза колебаний, w0– круговая (циклическая частота), t – время, 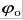 – начальная фаза колебаний. – начальная фаза колебаний.
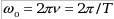 , ,
где V– частота колебаний, 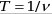 – период колебаний. – период колебаний.
- Скорость и ускорение при гармонических колебаниях
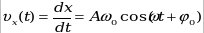 , ,
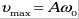 - амплитуда скорости (максимальное значение); - амплитуда скорости (максимальное значение);
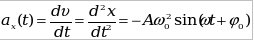 , ,
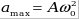 - амплитуда ускорения (максимальное значение). - амплитуда ускорения (максимальное значение).
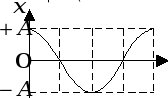
При ф0 = 0 графики зависимостей х(t), v(t), a(t) представлены на рис. 1(а,б,в), соответственно.
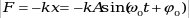 , ,
где 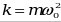 – коэффициент упругой (квазиупругой) силы, m – масса материальной точки; – коэффициент упругой (квазиупругой) силы, m – масса материальной точки;
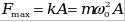 - амплитуда силы (максимальное значение). - амплитуда силы (максимальное значение).
- Кинетическая энергия колеблющейся точки
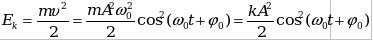
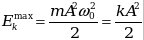 -амплитуда кинетической энергии (максимальное значение). -амплитуда кинетической энергии (максимальное значение).
а а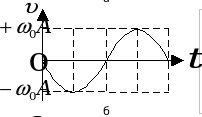
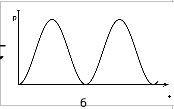
б б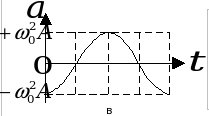
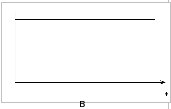
в в
Рис. 1 Рис. 2
- Потенциальная энергия колеблющейся точки
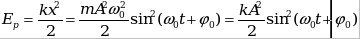
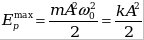 -амплитуда потенциальной энергии (максимальное значение). -амплитуда потенциальной энергии (максимальное значение).
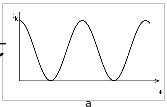
При ф0 = 0 графики зависимостей кинетической и потенциальной энергии от времени представлены на рис. 2а и 2б, соответственно.
- Полная энергия при гармонических колебаниях (рис. 2в)
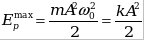 . .
- Уравнения гармонических колебаний могут быть заданы функциями синуса или косинуса. В таблице 1 даны значения скорости, ускорения, силы и энергии в обоих случаях.
Таблица 1
 – математический маятник (l– длина нити); – математический маятник (l– длина нити);
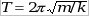 – пружинный маятник (m – масса тела, k– коэффициент жесткости); – пружинный маятник (m – масса тела, k– коэффициент жесткости);
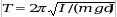 – физический маятник (I– момент инерции тела относительно оси, проходящей через точку подвеса, определяется по теореме Штейнера, m– масса тела,d– расстояние от точки подвеса до центра масс). – физический маятник (I– момент инерции тела относительно оси, проходящей через точку подвеса, определяется по теореме Штейнера, m– масса тела,d– расстояние от точки подвеса до центра масс).
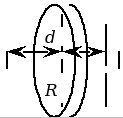
Пример: Однородный диск радиусом R = 0,2 м колеблется около горизонтальной оси, проходящей на расстоянии d = 0,15 м от центра диска. Определить период T колебаний диска относительно этой оси (рис. 3).
 Период определяется по формуле Период определяется по формуле 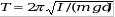 , где , где   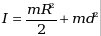 (нашли по теореме Штейнера). Тогда (нашли по теореме Штейнера). Тогда
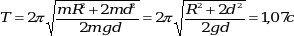 Рис. 3 Рис. 3
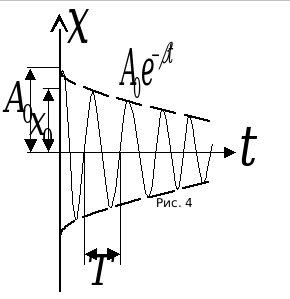
- Уравнение затухающих колебаний (рис. 4)
 , ,
где A0– амплитуда колебаний в начальный момент времени,B– коэффициент затухания, 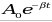 - зависимость амплитуды затухающих колебаний от времени, - зависимость амплитуды затухающих колебаний от времени, 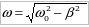 -частота затухающих колебаний, -частота затухающих колебаний, 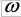 - частота собственных колебаний, - частота собственных колебаний, 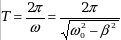 - период затухающих колебаний. - период затухающих колебаний.
- Уравнение вынужденных колебаний, совершаемых под действием периодически изменяющейся силы
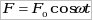
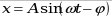 , где , где
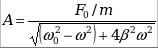 - амплитуда вынужденных колебаний; - амплитуда вынужденных колебаний;
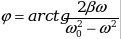 - начальная фаза вынужденных колебаний; - начальная фаза вынужденных колебаний;
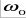 и и 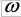 - частоты собственных и вынужденных колебаний . - частоты собственных и вынужденных колебаний .
- Резонанс – резкое возрастание амплитуды вынужденных колебаний при частоте, близкой к частоте собственных колебаний.
- Амплитуда при резонансе
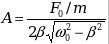 . .
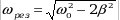 . .
Дифференциальные уравнения колебаний
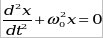 - гармонические, - гармонические,
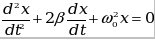 - затухающие, - затухающие,
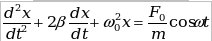 - вынужденные. - вынужденные.
- Уравнение колебания, полученного при сложении двух колебаний одинаковой частоты и одного направления, амплитуды колебаний которых A1 и A2, а начальные фазы A
- Ф1 и Ф2,
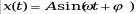 , где , где
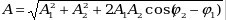 - -
амплитуда результирующего колебания, 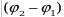 - разность фаз слагаемых колебаний; начальная фаза результирующего колебания определяется формулой - разность фаз слагаемых колебаний; начальная фаза результирующего колебания определяется формулой
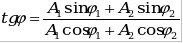 . .
- Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с одинаковыми частотами
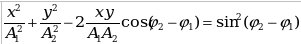 : :
а) если 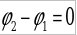 , то , то 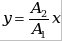 - уравнение прямой, - уравнение прямой,
б) если 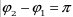 , то , то 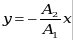 - уравнение прямой, - уравнение прямой,
в) если 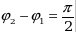 , то , то 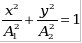 - уравнение эллипса, приведённого к осям, - уравнение эллипса, приведённого к осям,
г) если 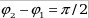 и и 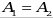 , то , то 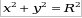 - уравнение окружности, где R- радиус окружности. - уравнение окружности, где R- радиус окружности.
|
