5.5. Дифференциальные уравнения конвективного теплообмена
Конвективный теплообмен определяется не только тепловыми, но и гидродинамическими явлениями. Поэтому при решении практически всех задач конвективного тепло- и массообмена сначала решают гидродинамическую задачу.
Математическое описание конвекции представляет собой объединение законов сохранения с соответствующими законами переноса. Гидродинамическое состояние системы выясняется решением известных из курса механики жидкостей и газов уравнений неразрывности и движения, которые для жидкости с постоянной вязкостью имеют вид:
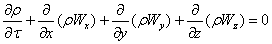; (5.21)
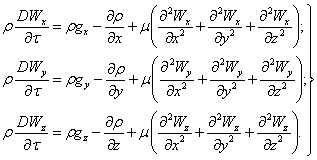(5.22)
Здесь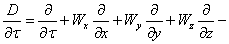 
полная или субстанциональная производная, характеризующая скорость изменения параметра в точке, движущейся вместе с жидкостью, 
, 
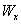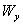и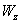 
- проекции скорости на сои координат; gx, gy и gz – проекции ускорения свободного падения на оси координат.
Уравнение (5.21) называют уравнением неразрывности; оно выражает закон сохранения массы. Уравнения Навье-Стокса (5.22) представляет собой закон сохранения импульса.
Так как у поверхности твердого тела есть тонкий слой малоподвижной жидкости, для него справедлив закон Фурье:
qст = λп(∂t/∂n) n = 0, (5.23)
где n – нормаль к поверхности тела. Из (5.23) и (5.19) получается дифференциальное уравнение теплообмена, описывающее процесс теплоотдачи на поверхности тела (n=0):
α = -[λп/(tст-tп)](∂t/∂n)n=0, (5.24)
То есть, чтобы найти коэффициент теплоотдачи, необходимо знать градиент температуры в жидкости, то есть знать температурное поле потока.
Уравнение энергии при конвективном теплообмене для случая движения газа (жидкости) с умеренными скоростями:
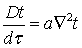, (5.25)
здесь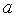 
– коэффициент температуропроводности; предполагается несжимаемость среды (ρ=const).
Таким образом, задача конвективного теплообмена описывается системой нелинейных дифференциальных уравнений в частных производных (5.21) - (5.25). Эта система имеет бесконечное множество решений. Чтобы получить единственное решение, нужно дополнить систему условиями однозначности.
- Геометрическими условиями, задающими размеры и форму поверхности тела, омываемого потоком жидкости, газа или пара. Такими условиями могут быть, например, диаметр d и длина канала l.
- Временными условиями, определяющими изменение процессов теплоотдачи во времени. При изучении конвективного теплообмена обычно задача предполагается стационарной, то есть режим процесса во времени не изменяется.
- Граничными условиями, которые определяют распределение температур и скоростей на поверхности твердого тела, участвующего в теплообмене. Очень часто распределение температур и скоростей на поверхности тела принимается равномерным. В этом случае коэффициент теплоотдачи будет одинаковым для всей поверхности.
- Физическими условиями, которые содержат данные о параметрах потока, входящих в дифференциальные уравнения: коэффициенте объемного расширения β, разности температур стенки и потока Δt и др.
