5.4. Конвективный теплообмен
Теплообмен на границе твердого тела и движущегося потока жидкости или газа осуществляется одновременно посредством теплопроводности и конвекции и называется конвективным теплообменом.
Конвективная передача тепла осуществляется за счет перемещения микро – и макрообъемов (вихрей), а молекулярная передача тепла – теплопроводностью в жидкостях и газах – за счет движения молекул. В большинстве случаев скорости движения вихрей выше скоростей молекул, и обычно конвекцией передаются большие количества тепла.
Различают вынужденную конвекцию (под действием внешних сил) и свободную, или естественную конвекцию (вызвана неоднородностями среды – градиентами температуры и плотности). Пример вынужденной конвекции – теплообмен между поверхностью твердого тела и движущимся потоком при воздействии на поток внешних сил. Пример свободной конвекции – теплообмен между поверхностью твердого тела и жидкостью или газом, которые перемещаются под влиянием разности плотностей нагретых и холодных частиц.
Количество тепла, передаваемое конвекцией стенке канала от жидкости или газа, определяется количеством вещества, перемещающегося по нормали к поверхности стенки. Оно зависит от режима движения (ламинарного или турбулентного).
При ламинарном режиме такой перенос тепла определяется только процессом молекулярного переноса вещества, зависящем от коэффициента теплопроводности жидкости или газа. При турбулентном режиме перенос обусловлен поперечным перемещением вихрей.
При приближении к стенке канала роль теплопроводности в передаче тепла возрастает, вблизи стенки влиянием конвекции можно вообще пренебречь. Дело в том, что внутри потока выделяют ядро и динамический пограничный слой в пристеночной части. Динамический пограничный слой состоит из двух подслоев – ламинарного и турбулентного; первый – находится вблизи стенки, второй – между ламинарным подслоем и ядром потока. В пределах ламинарного подслоя теплопередача осуществляется теплопроводностью, а во втором подслое, как и в ядре, конвекцией.
Толщина ламинарного подслоя зависит от скорости потока – чем она выше, тем больше интенсивность турбулентных вихрей и меньше толщина ламинарного подслоя.
Подобно изменению скорости происходит и изменение температуры в поперечном сечении потока. В турбулентном потоке сильнее всего температура меняется в пределах тонкого слоя, примыкающего к стенке канала. В этом слое, называемом температурным пограничным слоем, температура потока изменяется от ее значения в ядре до температуры стенки.
То есть на стенках канала существует два пограничных слоя – динамический и тепловой. Толщина первого уменьшается с ростом вязкости, второго – с ростом коэффициента теплопроводности среды. В жидкостях динамический слой толще теплового. В расплавленных металлах – наоборот. Для газов толщины этих слоев одинаковы.
Конечной целью любого теплотехнического расчета конвективного теплообмена является определение плотности теплового потока на поверхности qст.
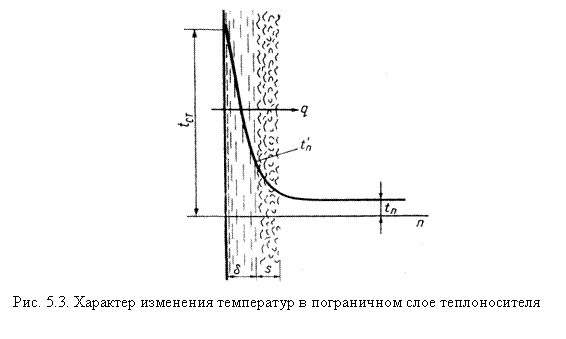
Рассмотрим для этого поле температур в турбулентном потоке. Характер изменения температур показан на рис. 5.3. Из рисунка видно, что в ламинарном подслое толщиной δ температура потока резко меняется от температуры стенки tст до температуры t'п. В турбулентном подслое толщиной s она подает от t'п до температуры потока tп.
Учитывая, что через ламинарный подслой тепло передается теплопроводностью, плотность потока можно определить на основе уравнения:
qст = λп(tст – t'п)/δ = - λ(gradt)ст. (5.18)
Измерить (gradt)ст или δ трудно, так как эти параметры зависят от режима движения, размеров и состояния поверхности нагрева и т.п. Поэтому конвективный теплообмен рассчитывают на основе закона Ньютона-Рихмана:
qст = α(tст – tп). (5.19)
Параметр α - коэффициент теплоотдачи – меняется в очень широких пределах, являясь гидродинамической характеристикой системы (в то время как разность температур – величина термодинамическая). Смысл применения уравнения (5.19) – в том, что во многих случаях плотность теплового потока qст почти прямо пропорциональна tст – tп. В случае нелинейных задач, когда сам α зависти от разности температур, использование коэффициента теплоотдачи не столь целесообразно.
Приравняв (5.18) и (5.19), можно получить:
α ≈ λп /δ. (5.20)
Это соотношение удобно использовать для качественной оценки влияния некоторых факторов на величину коэффициента теплоотдачи конвекцией. Например, увеличение скорости потока приведет к увеличению турбулентности и уменьшению толщины ламинарного подслоя и к увеличению коэффициента теплоотдачи. Увеличение вязкости потока приводит, наоборот, к возрастанию δ.