Специальные главы физики

5.3. Дифференциальное уравнение теплопроводности

При выводе используются следующие допущения:

1. тело однородно и изотропно;
2. физические параметры вещества постоянны и не зависят от температуры;
3. термическая деформация невелика и ею можно пренебречь;
4.  макроскопические частицы тела неподвижны относительно друг друга;
5. внутренние источники теплоты в теле распределены равномерно.

С физической точки зрения, дифференциальное уравнение теплопроводности представляет закон сохранения энергии:

dU = dQ_ист – dQ_выт,                 (5.9)

где dQ_ист – количество теплоты, создаваемое источником тепла внутри элементарного объема dV=dxdydz, dQ_выт – количество теплоты, вытекающее из данного объема (рис. 5.2).

dQ_ист = q_Vdxdydzdτ,      (5.10)

где  q_V – объемная мощность источников тепла внутри объема dV.

В направлении Х:

dQ_x  = q_xdydzdτ,            (5.11)

dQ_x+dx  = q_x+dxdydzdτ = (qx + 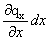)dydzdτ.        (5.12)

Учтем, что   q_x , тогда

dQ_{выт х} = dQ _х – dQ _x+dx = -(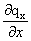)dxdydzdτ.=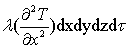. (5.13)

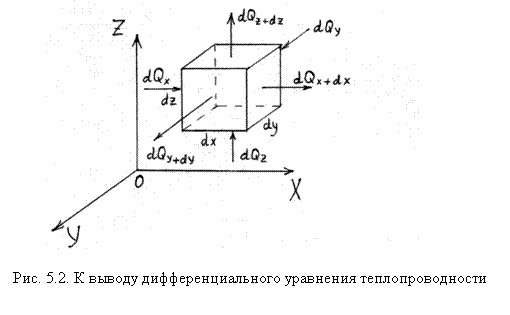
Аналогичные выражения справедливы по направлениям y и z. Таким образом, полное количество теплоты, вытекающее из объема dV по всем трем направлениям:

dQ_выт = 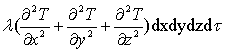,                 (5.14)

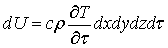.            (5.15)

Подставляя выражения (5.10), (5.14) и (5.15) в (5.9), получим:

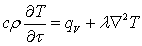,                  (5.16)

где 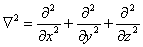- оператор Лапласа.

Разделив обе части равенства (5.16) на сρ и введя новую величину –      коэффициент температуропроводности 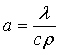 [м²/с], получим:

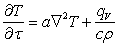.    (5.17)

Выражение (5.17) и представляет собой дифференциальное уравнение Фурье.

В частных случаях: при 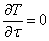 и q_V = 0 получаем уравнение Лапласа; при  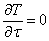и q_V ≠ 0 – уравнение Пуассона.