Специальные главы физики

5.2. Элементы аналитической теории теплопроводности твердых тел.
Закон Фурье

Основные понятия теории теплопроводности:

1. Температурное поле – совокупность значений температуры во всех точках изучаемого пространства для каждого момента времени. Для трехмерного температурного поля:

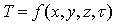, здесь τ – время.                                (5.1)

В общем случае поле нестационарно, то есть зависит от времени. Если же 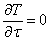 , то поле называется стационарным:  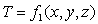(не зависит от времени).

Температурное поле также может быть двумерным:

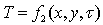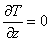;                                                    (5.2)

и одномерным:

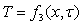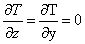; .                                                          (5.3)

2. Изотермическая поверхность – это геометрическое место точек, имеющих одинаковую температуру. Очевидно, что изотермические поверхности не пересекаются – они либо оканчиваются на поверхности тела, либо целиком располагаются внутри тела.
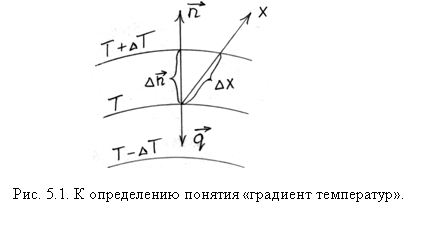
3. Градиент температуры – вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры:

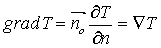,    (5.4)

здесь 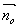- единичный вектор нормали к изотермической поверхности. В декартовых координатах:

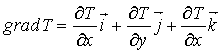,    (5.5)

здесь 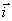,  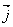и 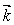- единичные векторы вдоль направлений x, y и z (рис. 5.1).

4. Тепловой поток. Закон Фурье
   

Необходимым условием распространения тепла в теле (это может быть твердое тело, жидкость или газ) является неравномерность распределения температуры внутри тела, то есть наличие градиента температуры. Это значит, что условие 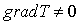 является основным физическим параметром, определяющим условия возникновения теплового процесса.

Фурье высказал гипотезу о том, что количество теплоты δQT, проходящее через элемент изотермической поверхности dF за время dτ, пропорционально градиенту температуры:

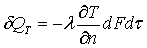,       (5.6)

где λ есть коэффициент теплопроводности. Введем вектор плотности теплового потока 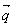 - вектор, модуль которого равен потоку тепла через единичное сечение, перпендикулярное  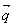(рис. 5.1), размерность q – Вт/м². Обычно уравнение (5.6) записывают в векторной форме через вектор плотности теплового потока:

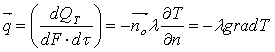.          (5.7)

Знак «–» в данном выражении соответствует противоположным направлениям векторов плотности теплового потока 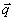 и gradT, то есть тепло течет в направлении убывания температуры (рис. 5.1).

Это и есть математическая запись закона Био-Фурье – закона распространения тепла посредством теплопроводности. Этот закон справедлив как для стационарных, так и для нестационарных процессов распространения тепла.

Однако, в случае высокоинтенсивных нестационарных процессов нарушается линейная связь между плотностью теплового потока 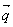 и gradT, и необходимо учитывать несинхронность изменения времени релаксации τ_р – то есть запаздывание перестройки температурного поля под действием изменившегося теплового потока. В этих случаях закон Био-Фурье имеет вид:

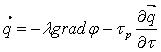.    (5.8)

Физический смысл коэффициента теплопроводности λ – он определяет количество теплоты, проходящее через единицу поверхности в единицу времени при изменении температуры в 1^о на единицу длины. λ зависит от многих факторов – от температуры, давления, структуры, влажности, плотности и т. д.

Примерные значения коэффициента теплопроводности: для газов составляет около 0,006-0,17 Вт/(м^оС), с повышением температуры он растет. Для капельных жидкостей значение λ лежит в пределах от 0,09 до 0,7 Вт/(м^оС), с повышением температуры он убывает для большинства жидкостей, за исключением воды. Для строительных и теплоизоляционных материалов  λ имеет значение от 0,02 до 3 Вт/(м^оС). Для металлов λ изменяется в пределах от 2,5 до 420 Вт/(м^оС); наилучшая теплопроводность – у Ag, Cu, Al, Au (как и электропроводность), с ростом температуры теплопроводность металлов уменьшается.