4.2. Вариационные принципы термодинамики и условия фазового равновесия.
В этом разделе мы будем использовать вариационные принципы термодинамики и понятие химического потенциала.
Принцип минимума свободной энергии: в системе, в которой протекает самопроизвольный необратимый процесс при постоянных температуре и объеме, свободная энергия F убывает и при достижении равновесия она минимальна
dF=0. (4.1)
Принцип минимума термодинамического потенциала Гиббса: в системе, где протекает самопроизвольный процесс при постоянных температуре и давлении термодинамический потенциал Гиббса убывает и при равновесии минимален
dG=0. (4.2)
Химический потенциал можно определить выражениями:
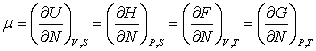. (4.3)
Химический потенциал есть мера изменения термодинамических функций в зависимости от числа частиц в системе N. Особое место среди термодинамических функций занимает термодинамический потенциал Гиббса G(P,T,N), аргументы которого Р и Т не аддитивны. Его можно представить в виде
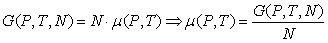; (4.4)
таким образом, химический потенциал μ представляет удельный потенциал Гиббса – то есть потенциал Гиббса, приходящийся на одну частицу. Для многокомпонентной системы
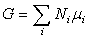, (4.5)
где Ni – количество частиц i-го компонента системы.
Химический потенциал не аддитивен, он является интенсивной величиной, также как температура, давление, плотность,, и не зависит от числа частиц системы. Экстенсивные величины зависят от числа частиц – это энергия, энтропия, количество вещества, заряд и т. д.
Теперь рассмотрим условия равновесия фаз для двухкомпонентной системы. Очевидно, что температуры и давления подсистем равны (Р1 = Р2, Т1 = Т2). Третье условие получим из принципа минимума потенциала Гиббса G (P, T, N1, N2):
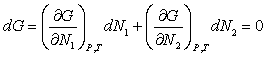. (4.6)
Поскольку dN1= – dN2, следовательно
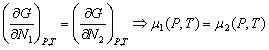. (4.7)
Уравнение (4.7) выражает условие фазового равновесия для системы, состоящей из двух фаз. Это уравнение определяет кривую фазового равновесия. На рис. 4.1 приведена кривая фазового равновесия для двухфазной системы жидкость-газ.
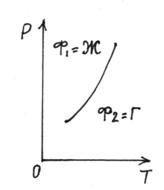
Рис. 4.1. Кривая фазового равновесия для системы жидкость-газ
Примером трехфазной системы может служить система лед-вода-пар (твердое тело-жидкость-газ). Для такой системы условия равновесия выглядят так:
Т1 = Т2 = Т3, Р1 = Р2 = Р3 и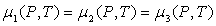 
. (4.8)
По сути дела последнее равенство представляет собой систему уравнений для поиска двух неизвестных – Т и Р. Эта система разрешима и однозначно определяются те Т и Р, при которых могут находиться в равновесии три фазы вещества: твердая, жидкая и газообразная. Соответствующая точка на диаграмме (Р, Т) называется тройной точкой. Кривые плавления, испарения и сублимации разбивают координатную плоскость на три области – слева от кривых сублимации и плавления лежит область твердой фазы, между кривыми плавления и испарения заключена область жидких состояний; справа от кривых испарения и сублимации расположена область газообразных состояний вещества (рис. 4.2). Любая точка в одной из этих областей изображает соответствующее однофазное состояние вещества; точка, лежащая на одной из кривых – состояние равновесия двух соответствующих фаз вещества; тройная точка – состояние равновесия всех трех фаз.
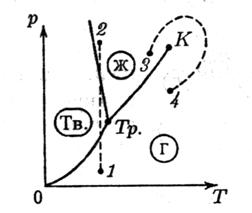
Рис. 4.2. Диаграмма состояния для системы твердое тело-жидкость-газ
