3.2. Метод термодинамических функций
Это метод получения термодинамической информации об изучаемых телах, основанный на использовании так называемых термодинамических потенциалов, или термодинамических функций. Каждому набору независимых параметров соответствует свой термодинамический потенциал.
Для реализации этого подхода прежде всего необходимо выбрать независимые параметры, которые можно задавать произвольно, а через них выражать другие величины. В наиболее простых случаях такими параметрами являются :
объем V и давление Р – это механические переменные;
температура Т и энтропия S – это термические переменные.
Между этими величинами в принципе существуют два уравнения связи:
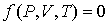 - термическое уравнение; - термическое уравнение;
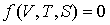 - калорическое уравнение. - калорическое уравнение.
Например, для идеального газа
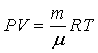 - термическое уравнение - термическое уравнение
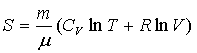 - калорическое уравнение. - калорическое уравнение.
Благодаря двум уравнения связи число независимых переменных снижается с четырех до двух. Их следует выбирать так, чтобы одна была механическая, а другая – термическая. Таким образом, возможны четыре различных сочетания параметров, соответствующих различным термодинамическим потенциалам:
Независимые
переменные |
V, S |
P, S |
V, T |
P, T |
Зависимые переменные |
P, T |
V, T |
P, S |
V, S |
Термодинамический потенциал |
U(V, S)
внутренняя энергия |
H(P, S)
энтальпия |
F(V, T)
свободная энергия, или энергия Гельмгольца |
G(P, T)
термодина-мический потенциал
Гиббса |
Остановимся подробнее на каждом из данных потенциалов.
Внутренняя энергия. Внутренняя энергия системы вводится через первое начало термодинамики
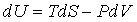 . (3.8) . (3.8)
В качестве так называемых естественных переменных для потенциала U выступают переменные S и V. Из (3.8) следует:
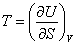 (3.9); (3.9);
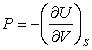 (3.10); (3.10);
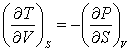 (3.11) (3.11)
Энтальпия. При изобарном нагревании количество получаемой телом теплоты
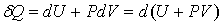 . .
Термодинамическую функцию
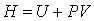 (3.12) (3.12)
называют энтальпией или тепловой функцией. Ее полный дифференциал равен
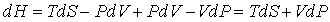 . (3.13) . (3.13)
Из (3.12) следует:
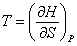 (3.14); (3.14);
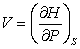 (3.15); (3.15);
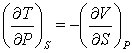 (3.16) (3.16)
Свободная энергия. Работа, производимая телом при обратимом изотермическом процессе
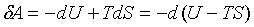 . .
Термодинамическую функцию
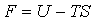 (3.17) (3.17)
называют свободной энергией тела.
Ее полный дифференциал равен
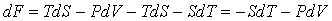 . (3.18) . (3.18)
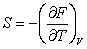 (3.19); (3.19); 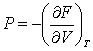 (3.20); (3.20); 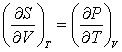 (3.21) (3.21)
Термодинамический потенциал Гиббса. Эта функция определяется выражением
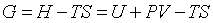 . (3.22) . (3.22)
Ее полный дифференциал равен
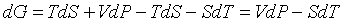 . (3.23) . (3.23)
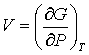 (3.24); (3.24); 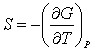 (3.25); (3.25); 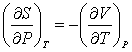 (3.26) (3.26)
Можно показать, что все четыре функции U, H, F и G – аддитивные, что делает их гибким и удобным инструментом термодинамических исследований.
Рассмотрим пример применения метода термодинамических функций.
Этот метод состоит в том, что если известна одна из четырех функций, то из нее можно получить весь объем термодинамической информации о системе.
Например, исходя из свободной энергии F(V,T), получим выражение для коэффициента теплового расширения:
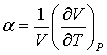 . (3.27) . (3.27)
Для поиска 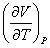 используем (3.20): используем (3.20):
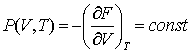 (3.28) (3.28)
Считая Т аргументом, а V=f(T), продифференцируем (3.28) по Т:
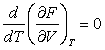 . (3.29) . (3.29)
Отсюда
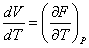 . (3.30) . (3.30)
Подставляя (3.30) в (3.27), получаем искомое выражение для коэффициента теплового расширения.
|