3.1. Характеристики термодинамических систем и процессов. Энтропия
Термодинамика изучает наиболее общие закономерности превращения энергии в макроскопических системах. При этом не интересуются микрохарактеристиками, состоянием и движением отдельных частиц, и ограничиваются установлением связей между непосредственно измеряемыми макроскопическими величинами ( это такие величины, как объем V, температура Т, давление Р и т. д.), основываясь на двух весьма общих абсолютно верных основополагающих принципах (законах, началах). Термодинамический метод дает простейшие варианты решения многих практических задач и положен в основу ряда таких прикладных наук, как, например, теплотехника.
Основные понятия термодинамики:
Термодинамическая система – совокупность макроскопических тел любой физико-химической природы, между которыми возможен теплообмен.
Термодинамическое состояние характеризуется определенной совокупностью термодинамических параметров (внешних – это объем, электрическое поле и т. д. И внутренних – это давление, поляризация и т. д. ). Различают стационарные и нестационарные, равновесные и неравновесные состояния.
Термодинамический процесс – всякое изменение в системе хотя бы одного из макроскопических параметров. Процессы бывают прямые, обратные и круговые. Равновесный процесс (статический) – это любое промежуточное состояние равновесия (абстракция).
Первое начало термодинамики представляет собой специфическую форму закона сохранения энергии:
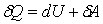 , (3.1) , (3.1)
где 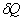 - элементарная теплота, - элементарная теплота, 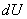 - приращение внутренне энергии, - приращение внутренне энергии, 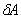 - элементарная работа. - элементарная работа.
Второе начало термодинамики имеет несколько эмпирических формулировок. Наиболее простая – формулировка Томсона:
невозможно полностью преобразовать в работу теплоту какого-либо тела, не совершая никакого другого действия, кроме охлаждения этого тела.
Отсюда вывод – КПД тепловых машин принципиально не может быть больше единицы и невозможна тепловая машина, которая бы полностью преобразовывала теплоту в работу, то есть вечный двигатель второго рода.
Для характеристики термодинамического состояния системы и его изменения в различных процессах Клаузиус ввел термодинамическую величину энтропия S через ее элементарное приращение
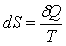 . (3.2) . (3.2)
При переходе из одного состояния в другое изменение этой величины определяется интегралом:
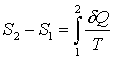 . (3.3) . (3.3)
При этом сам процесс, то есть способ перехода из состояния 1 в состояние 2 не играет роли. Важно, чтобы состояния были равновесными. Для кругового процесса 1-2-1 справедливо неравенство
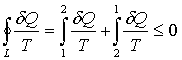 , (3.4) , (3.4)
которое выражает теорему Клаузиуса. Здесь знак «=» - для обратимых процессов, а знак «<» - для необратимых.
Основные свойства энтропии:
- Она является функцией состояния – то есть не зависит от способа перехода из одного состояния в другое.
- Аддитивность – энтропия макросистемы равна сумме энтропий отдельных частей системы.
- Энтропия замкнутой (то есть не обменивающейся с внешней средой ни энергией, ни веществом) системы не может убывать – она либо возрастает, либо постоянна. Это фактически еще одна формулировка второго закона термодинамики, наиболее полная с теоретической точки зрения, или закон возрастания энтропии.
Величина возрастания энтропии в замкнутой системе служит мерой необратимости протекающих в системе процессов. Если все процессы обратимы, то S = const.
- При T->0, S->0.
Это теорема Нернста, или третье начало термодинамики.
Отсюда величину энтропии можно вычислить по формуле:
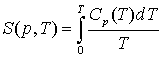 , (3.5) , (3.5)
здесь СР – теплоемкость при постоянном объеме. При этом СР -> 0 при T -> 0; этот интеграл не сходится.
С использованием понятия энтропии первое начало термодинамики можно записать следующим образом:
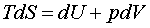 , (3.6) , (3.6)
это основное уравнение термодинамики имеет многочисленные применения.
Вероятностный смысл энтропии определяется формулой Больцмана:
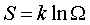 . (3.7) . (3.7)
Здесь k – постоянная Больцмана, Ω – термодинамическая вероятность, равная числу способов реализации данного макросостояния, то есть число микросостояний в данном макросостоянии. Из принципа возрастания энтропии Больцман сделал фундаментальный вывод:
все замкнутые макросистемы стремятся переходить от менее вероятных состояний к более вероятным.
Следует отметить, что физический смысл второго начала термодинамики тесно связан с принципом Ле-Шателье-Брауна, который справедлив для всех макросистем:
Если посредством внешнего воздействия система выводится из равновесного состояния, то в системе возникают процессы, направленные на ослабление этого воздействия.
|