2.2.2. Основы зонной теории кристаллов
Рассматривая ранее задачу о движении электрона в металле, мы сделали существенное допущение – предположили, что электроны проводимости являются свободными. В действительности в кристалле каждая частица (электрон или ядро) взаимодействует с огромным количеством других частиц и точное решение уравнения Шредингера для такой системы частиц невозможно.
Для приближенного решения квантовых задач о поведении электронов в кристалле оказалось весьма плодотворным одноэлектронное приближение, когда рассматривается движение одного электрона в поле эффективного потенциала, учитывающего поле ионов и самосогласованное усредненное поле остальных электронов системы. При этом используются следующие допущения.
- Из-за значительной разницы в массах электронов и ядер скорости движения этих частиц совершенно различны, поэтому ядра можно считать по сравнению с электронами неподвижными. То есть электрон движется в поле неподвижных ядер.
- Медленное движение ядер рассматривается в усредненном поле всех электронов.
- Сложное взаимодействие каждого отдельного электрона со всеми остальными рассматривается как взаимодействие его с самосогласованным полем, создаваемым усредненным пространственным распределением заряда этих электронов. В таком эффективном поле каждый электрон движется независимо.
 С такими упрощениями решение уравнения Шредингера о движении электрона в металле становится возможным и дает допустимые значения энергии свободных электронов в кристалле. При этом необходимо учитывать принцип Паули. С такими упрощениями решение уравнения Шредингера о движении электрона в металле становится возможным и дает допустимые значения энергии свободных электронов в кристалле. При этом необходимо учитывать принцип Паули.
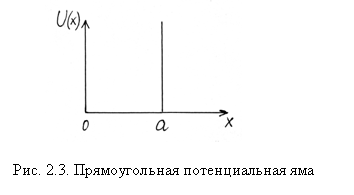
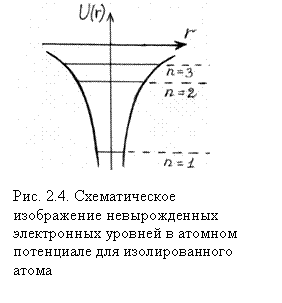
Чтобы понять происхождение энергетических зон в твердом теле, рассмотрим сначала процесс объединения атомов в кристалл. Изолированный атом представляет собой для электронов потенциальную яму (рис. 2.3); как известно, энергетический спектр для частицы в потенциальной яме дискретный, поэтому энергия электрона в атоме может принимать лишь вполне определенные значения. На рис. 2.4 показана схема невырожденных (нерасщепленных) энергетических уровней для изолированного атома. Напомним, что вырожденными называются состояния с одинаковой энергией, а число разных состояний с каким-либо значением энергии называется кратностью вырождения соответствующего энергетического уровня.
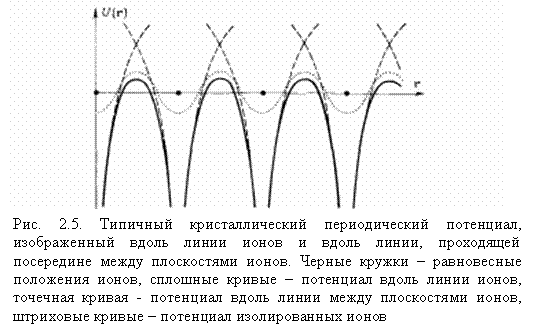
 Пусть имеется N изолированных атомов какого-либо вещества. Пока атомы изолированы друг от друга, они имеют полностью совпадающие схемы энергетических уровней. Заполнение уровней электронами идет в каждом атоме независимо от заполнения аналогичных уровней в других атомах. Если среднее расстояние между атомами d > 10-9 м, то уровни в атомах практически не изменяются. По мере сближения атомов (при d < 10-9 м) между ними возникает все усиливающееся взаимодействие, высота потенциального барьера снижается за счет притяжения соседних ядер. На рис. 2.5 показан периодический кристаллический потенциал для случая одномерного кристалла. В кристалле разность между полной энергией электрона в атоме и высотой потенциального барьера мала, а сам барьер достаточно узок, что благоприятно для реализации туннельного перехода из одного атома в соседний. Причем вероятность туннелирования велика именно для валентных электронов и чрезвычайно мала для электронов внутренних оболочек (так называемых остовных электронов). То есть, валентные электроны не локализованы возле атомов, а как бы «размазаны» по кристаллу – переходят от узла к узлу решетки. Пусть имеется N изолированных атомов какого-либо вещества. Пока атомы изолированы друг от друга, они имеют полностью совпадающие схемы энергетических уровней. Заполнение уровней электронами идет в каждом атоме независимо от заполнения аналогичных уровней в других атомах. Если среднее расстояние между атомами d > 10-9 м, то уровни в атомах практически не изменяются. По мере сближения атомов (при d < 10-9 м) между ними возникает все усиливающееся взаимодействие, высота потенциального барьера снижается за счет притяжения соседних ядер. На рис. 2.5 показан периодический кристаллический потенциал для случая одномерного кристалла. В кристалле разность между полной энергией электрона в атоме и высотой потенциального барьера мала, а сам барьер достаточно узок, что благоприятно для реализации туннельного перехода из одного атома в соседний. Причем вероятность туннелирования велика именно для валентных электронов и чрезвычайно мала для электронов внутренних оболочек (так называемых остовных электронов). То есть, валентные электроны не локализованы возле атомов, а как бы «размазаны» по кристаллу – переходят от узла к узлу решетки.
При рассмотрении образования энергетических зон в кристалле необходимо учитывать соотношение неопределенностей Гейзенберга, которое гласит: произведение неопределенностей времении энергии частицы не может быть по порядку величины меньше постоянной Планка
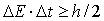 . (2.25) . (2.25)
Здесь 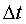 - время нахождения электрона в состоянии с энергией Е± - время нахождения электрона в состоянии с энергией Е± ; ; 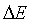 называется шириной энергетического уровня. называется шириной энергетического уровня.
В изолированном атоме время жизни невозбужденного энергетического уровня стремится к бесконечности, поэтому 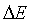 стремится к нулю. В возбужденном состоянии стремится к нулю. В возбужденном состоянии 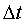 ≠ 10-8 с, а ≠ 10-8 с, а 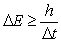 ≠ 10-7 эВ. ≠ 10-7 эВ.
В кристалле время пребывания валентного электрона в данном узле решетки при средней скорости электронов 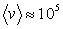 м/с и размерах атома около 10-10 м м/с и размерах атома около 10-10 м 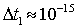 с. С помощью соотношения неопределенностей можно оценить неопределенность энергии электрона в кристалле: с. С помощью соотношения неопределенностей можно оценить неопределенность энергии электрона в кристалле: 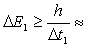 1 эВ. 1 эВ.
Таким образом, при образовании кристалла из N отдельных атомов вместо одного одинакового для всех уровня возникают N очень близких, но не совпадающих уровней. Каждый уровень изолированного атома расщепляется в кристалле на N густо расположенных уровней, образующих зону.
Если уровень, из которого образовалась зона, невырожденный, то число уровней в энергетической зоне кристалла равно числу атомов, входящих в кристалл. Если данный уровень вырожден, то число уровней в энергетической зоне равно произведению числа атомов кристалла на кратность вырождения.
Величина расщепления для разных уровней не одинакова. На рис. 2.6 показано расщепление уровней как функция расстояния r между атомами. Из схемы видно, что сильнее возмущаются (расщепляются) уровни, заполненные в атоме валентными электронами. Уровни, заполненные внутренними электронами, возмущаются мало. В зависимости от конкретных свойств атомов равновесное расстояние между соседними атомами в кристалле может быть либо типа r1, либо типа r2 (см. рис. 2.6). При расстоянии типа r1 между разрешенными зонами, возникшими из соседних уровней атома, есть запрещенная зона. При r2 происходит перекрывание соседних зон. Число уровней в такой слившейся зоне равно сумме количеств уровней, на которые расщепляются оба уровня.
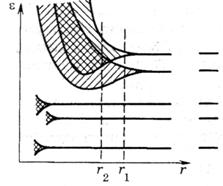
Рис. 2.6. Зависимость расщепления энергетических уровней от межатомного расстояния
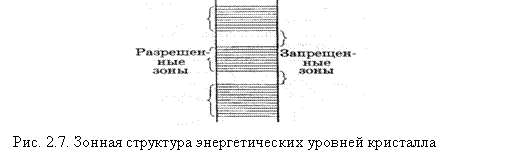
Таким образом, наличие в кристалле периодического поля решетки приводит к тому, что спектр возможных значений энергии валентных электронов распадается на ряд чередующихся разрешенных и запрещенных зон (рис. 2.7). В пределах разрешенных зон энергия изменяется квазинепрерывно. Значения энергии, принадлежащие запрещенным зонам, не могут реализоваться.
Рассматривая движение электронов в кристалле как волновое, можно получить связь энергии электрона Е с волновым числом k =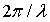 : :
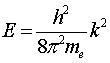 . (2.26) . (2.26)
Используя условие брэгговского отражения 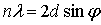 при угле дифракции φ, равном при угле дифракции φ, равном 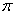 /2, получим условие для волнового числа к: /2, получим условие для волнового числа к:
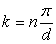 , n = 1, 2, 3, …. (2.27) , n = 1, 2, 3, …. (2.27)
При таких значениях волнового числа создаются условия для образования стоячих волн. Это такое состояние электрона, при котором он может с одинаковой вероятностью двигаться в прямом или обратном направлении. Перейти из этого состояния в другое с более высокой энергией и большим значением k электрон может только при скачкообразном изменении своей энергии на величину 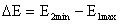 . .
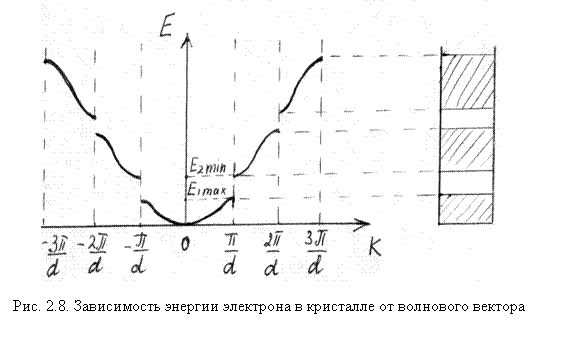
На рис. 2.8 изображена зависимость энергии электрона в кристалле от волнового числа k. Заштрихованные зоны квазинепрерывно изменяющейся энергии чередуются с запрещенными зонами. Область k– пространства (пространства волновых векторов), внутри которой энергия электрона изменяется квазинепрерывно, называется зоной Бриллюэна. На границах зон энергия терпит разрыв. Рис. 2.8 изображает зоны Бриллюэна для одномерного кристалла.
|