2.2.1. Квантовая статистика электронов
Свободные (валентные) электроны в металле обладают резко выраженными квантовыми свойствами. В основе квантовой теории металлов лежат следующие принципы:
- Все электроны в системе неразличимы.
- Энергия электронов квантована. Состояние каждого электрона определяется четырьмя квантовыми числами (n, l, ml, ms); изменение состояния электрона происходит при изменении хотя бы одного из них.
- Свободные электроны в металле подчиняются принципу запрета Паули: в одной и той же квантовой системе не может быть двух электронов, обладающих одинаковой совокупностью квантовых чисел. Иными словами, в системе не может быть более одного электрона в данном квантовом состоянии. Обладать одинаковой энергией (находиться на одном энергетическом уровне) могут не более двух электронов с противоположно направленными спинами (напомним, что спин – это собственный момент импульса).
Если в классической теории считалось, что при абсолютном нуле и в отсутствии других внешних возбуждений энергия всех свободных электронов равна нулю (то есть все электроны находятся в одном квантовом состоянии), то в квантовой теории такое невозможно (по принципу Паули) – свободные электроны при 0 К должны находиться в различных состояниях и заполнять попарно энергетические уровни в разрешенной зоне, начиная с самого низшего до самого высокого, на каждом уровне – два электрона, отличающихся лишь направлением спина (рис. 2.1,а). Предельный уровень энергии определяется числом свободных электронов – если имеется N свободных электронов, то число занятых уровней равно N/2. В этом случае говорят, что электронный газ полностью «вырожден». Энергетический уровень, который отделяет полностью заполненные уровни от полностью незаполненных при 0 К, называется уровнем Ферми и обозначается EF. Ферми и Дирак нашли вид функции распределения электронов по энергиям, которая хорошо описывает поведение электронов как при низких, так и при высоких температурах. Эта функция называется функцией распределения Ферми-Дирака и имеет вид
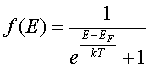 . (2.17) . (2.17)
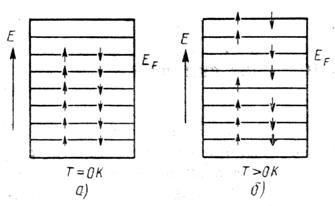
Рис. 2.1. Распределение электронов по энергетическим уровням при Т = 0 К
и Т > 0 К. Маленькими стрелками показаны направления спинов электронов
Физический смысл функции распределения: она показывает вероятность заполнения электронами энергетического уровня с энергией Е в условиях термодинамического равновесия электронов в системе. Здесь EF – энергия Ферми или уровень Ферми.
Физический смысл уровня Ферми можно понять, рассматривая функцию Ферми вблизи 0 К:
для Е > EF f(E) -> 0 (уровни не заняты) |
для Е < EF f(E) -> 1 (уровни заняты) |
Таким образом, физический смысл энергии Ферми – это максимальное значение энергии, которое может иметь электрон в металле при 0 К.
Повышение температуры выше 0 К влияет только на электроны, находящиеся вблизи уровня Ферми, которые возбуждаются и переходят в соседние более высокие незанятые состояния (рис. 2.1, б). «Вырождение» постепенно снимается. Электроны, находящиеся на более низких энергетических уровнях, в силу принципа Паули, не могут принимать участия в тепловом движении – им необходимо при повышении температуры перейти на следующие более высокие уровни, а они заняты.
Графический вид функции Ферми при 0 К и более высоких температурах показан на рис. 2.2. Можно видеть, что при повышении температуры распределение в виде ступеньки, имеющее место при 0 К, вблизи Е = EF размывается и появляется вероятность заселения электронами состояний, находящихся выше EF. Размытие графика при Т > 0 К имеет величину порядка kТ.
Допустим, что электроны проводимости движутся в пределах образца металла совершенно свободно. В модели свободных электронов волновая функция электронов должна удовлетворять уравнению Шредингера с U=0
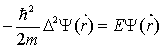 , (2.18) , (2.18)
m – масса, Е – энергия электрона.
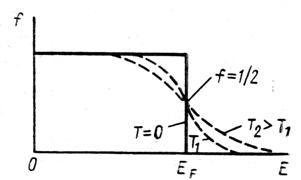
Рис. 2.2. Распределение электронов по энергиям при различных температурах
Решением данного уравнения является волновая функция вида
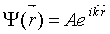 , (2.19) , (2.19)
здесь 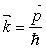 - волновой вектор электрона, связанный с энергией соотношением - волновой вектор электрона, связанный с энергией соотношением
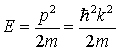 . (2.20) . (2.20)
Пусть концентрация свободных электронов в металле равна n. Тогда в образце объемом V будет содержаться nV свободных электронов. По принципу Паули, при абсолютном нуле они распределятся попарно на самых низких энергетических уровнях (на каждом уровне – два электрона, отличающихся направлением спина). Поэтому все состояния с энергией Е, меньшей некоторого значения ЕF(0), будут заняты, состояния же с Е > ЕF(0) – вакантными. Поверхность постоянной энергии в так называемом обратном пространстве, или k – пространстве (или в p – пространстве, 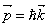 ), соответствующая значению энергии, равному ЕF, называется поверхностью Ферми. ), соответствующая значению энергии, равному ЕF, называется поверхностью Ферми.
Для свободных электронов эта поверхность описывается уравнением
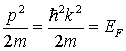 . (2.21) . (2.21)
и, следовательно, имеет форму сферы. При абсолютном нуле поверхность Ферми отделяет состояния, заполненные электронами, от незаполненных состояний.
Металлический образец представляет собой для электронов трехмерную потенциальную яму. Решение уравнения Шредингера для частицы, находящейся в такой яме, показывает, что энергия частицы может иметь только дискретные, или квантованные значения (задача о поведении частицы в потенциальной яме рассматривалась на 2 курсе в разделе «Квантовая физика»). В результате ее решения, применительно к нашему случаю с учетом всех электронов образца и граничных условий (ведь движение электронов ограничено объемом металла V), можно получить для энергии Ферми выражение
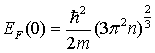 . (2.22) . (2.22)
Оценим значение EF(0). Концентрация свободных электронов в металлах n лежит в пределах от 1028 до 1029 м-3. Взяв для n среднее значение 5*1028 м-3, получим
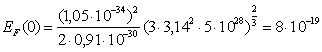 Дж = 5 эВ. Дж = 5 эВ.
А средняя энергия свободных электронов при 0 К оказывается равной
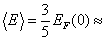 3 эВ. 3 эВ.
Это огромная величина. Для того, чтобы сообщить классическому электронному газу такую энергию, нужно нагреть его до температуры порядка 25000 К!
В то же время средняя энергия теплового движения, равная по порядку величины kT, при комнатной температуре составляет около 1/40 эВ. Такая энергия может возбудить лишь электроны, находящиеся на самых верхних уровнях, примыкающих к уровню Ферми. Поэтому основная масса электронов, размещенных на более низких уровнях, не поглощает энергию при нагревании и не участвует в теплоемкости. Этим и объясняется малая теплоемкость электронного газа в металлах.
Число электронов, участвующих в нагревании и обусловливающих тем самым теплоемкость, равно
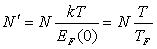 . (2.23) . (2.23)
Здесь параметр 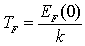 называется температурой Ферми. В результате теплоемкость электронов составит называется температурой Ферми. В результате теплоемкость электронов составит
СVэл ≈ СVкл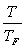 . (2.24) . (2.24)
При комнатной температуре Т ≈ 300 К СVэл примерно в 100 раз меньше СVкл
(т. к. ТF ≈ 30000 К). При таких температурах теплоемкость металлов будет определяться теплоемкостью, связанной с колебаниями решетки. Это хорошо согласуется с экспериментом – как отмечалось выше, теплоемкость металлов мало отличается от теплоемкости неметаллических кристаллов. Только вблизи абсолютного нуля теплоемкость решетки падает быстрее электронной теплоемкости и становится существенным вклад электронов в теплоемкость.
|