2.1.2. Объяснение законов Ома, Джоуля-Ленца, Видемана-Франца в
класической электронной теории
Классическая теория металлов Друде-Лоренца позволила объяснить законы Ома, Джоуля-Ленца, Видемана-Франца.
Закон Ома. Если электрон ускоряется полем, то получает от него дополнительную энергию. При соударении электрона с ионом решетки эта энергия передается иону и скорость электрона u после соударения равна нулю. Под действием поля с напряженностью Е электрон получает постоянное ускорение
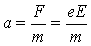 . (2.3) . (2.3)
К концу пробега скорость u достигнет в среднем значения
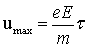 , (2.4) , (2.4)
где τ – среднее время между двумя последовательными соударениями электрона с ионами решетки; τ = λ/v, где λ – средняя длина свободного пробега электрона.
Так как скорость u изменяется за время пробега линейно, ее среднее за пробег значение равно половине максимального
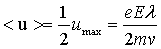 . (2.5) . (2.5)
Подставив (2.5) в (2.2), получим
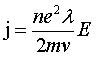 . (2.6) . (2.6)
Обозначив множитель 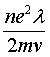 = σ, получим закон Ома в дифференциальной форме = σ, получим закон Ома в дифференциальной форме
j = σ E. (2.7)
где σ имеет смысл удельной электрической проводимости вещества.
Закон Джоуля-Ленца.Электрон, двигаясь под действием стационарного электрического поля Е от одного столкновения с ионом решетки до следующего столкновения приобретает дополнительную кинетическую энергию, среднее значение которой, согласно формуле (2.5), можно выразить
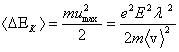 . (2.8) . (2.8)
Эта энергия полностью передается решетке и проявляется в нагревании металла. Согласно МКТ среднее число соударений электрона с узлами решетки
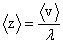 , (2.9) , (2.9)
тогда при концентрации свободных электронов n средняя удельная тепловая мощность тока (тепловая энергия, выделяющаяся за единицу времени в единице объема) равна
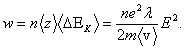 (2.10) (2.10)
Как видим, коэффициент перед Е 2 совпадает с определенным выше выражением для σ. Пользуясь соотношениями (2.7) и 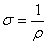 (где ρ – удельное сопротивление), получим (где ρ – удельное сопротивление), получим 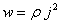 - закон Джоуля-Ленца в дифференциальной форме. - закон Джоуля-Ленца в дифференциальной форме.
Закон Видемана-Франца. Металлы наряду с высокой электропроводностью обладают большой теплопроводностью. Видеман и Франц установили в 1853 г эмпирический закон, согласно которому отношение теплопроводности ? к электропроводности σ для всех металлов примерно одинаково и изменяется пропорционально температуре
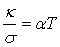 , (2.11) , (2.11)
где α – эмпирический коэффициент, зависящий от природы металла.
Считая электроны одноатомным газом, имеем:
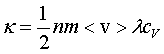 , (2.12) , (2.12)
где сV – удельная теплоемкость. Для одноатомного газа
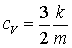 . (2.13) . (2.13)
Тогда
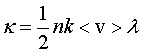 . (2.14) . (2.14)
Разделив к на σ и заменив затем (1/2)mv2 на (3/2)kT, получим
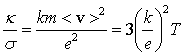 , (2.15) , (2.15)
которое выражает закон Видемана-Франца.
Итак, классическая электронная теория металлов позволила объяснить законы Ома, Джоуля-Ленца, Видемана-Франца. Но вместе с тем она встретилась с существенными затруднениями.
Например, электронный газ (как одноатомный) должен иметь молярную теплоемкость СV = (3/2)R. По закону Дюлонга и Пти, молярная теплоемкость простых тел одинакова и равна 3R. Следовательно, молярная теплоемкость металла равна:
СV = (3/2)R+3R = (9/2)R. (2.16)
То есть по классической теории, молярная теплоемкость металлов должна быть в 1,5 раза больше, чем у диэлектриков, не имеющих свободных электронов. В действительности же теплоемкость металлов не отличается заметно от неметаллических кристаллов. Кроме того, классическая теория не смогла объяснить самого главного – почему электроны в металлах оказываются свободными. Объяснение этого и других несоответствий смогла дать лишь квантовая теория металлов, основанная не на классической электронной статистике Максвелла-Больцмана, а на квантовой статистике Ферми-Дирака.
|