2.1.1. Модель свободных электронов
Как известно, по величине электропроводности все твердые тела можно разделить на три большие группы: металлы, полупроводники и диэлектрики. Более половины известных в настоящее время химических элементов относятся к металлам, которые являются прекрасными проводниками электрического тока.
Ток в металлах можно вызвать приложением крайне малой разности потенциалов – это значит, что носители тока (электроны), перемещаются по металлу практически свободно. Исходя из представлений о свободных электронах Друде и Лоренцем была развита классическая теория металлов.
Согласно этой теории, металл – совокупность кристаллической решетки, в узлах которой находятся положительно заряженные ионы, и электронов проводимости. Они предположили, что электроны проводимости в металле в отсутствии электрического поля ведут себя подобно молекулам идеального газа, движутся хаотически, но сталкиваются преимущественно не друг с другом, а с ионами решетки. Считается, что отсутствует взаимодействие электронов между собой (приближение независимых электронов) и не учитывается влияние положительно заряженных ионов на движение электронов в промежутках между столкновениями (приближение свободных электронов).
Полагая, что к электронному газу можно применить кинетическую теорию газов, оценим среднюю скорость теплового движения электронов по формуле:
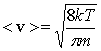 (2.1) (2.1)
Для комнатной температуры (300К) получим
 . .
При включении поля на хаотическое тепловое движение, происходящее со скоростью <v>, накладывается упорядоченное движение электронов с некоторой средней скоростью <u>. Значение этой скорости легко оценить из формулы
j=ne<u>, (2.2)
где j – плотность тока, n – концентрация свободных электронов в металле (примерно 1029м-3). Так как предельно допустимая плотность тока для медных проводов составляет около 107 А/м2, получим
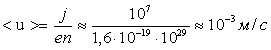
То есть даже при больших плотностях тока средняя скорость упорядоченного движения зарядов <u> в 108 раз меньше скорости теплового движения <v>.
|