1.4. Кристаллографические системы (сингонии)
Как уже говорилось ранее, решетку можно описать с помощью периодически повторяющегося в пространстве элементарного параллелепипеда – элементарной ячейки, построенной на трех векторах переноса, или единичных трансляциях 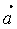 ,  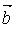,  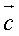. По форме элементарной ячейки – в зависимости от углов между ее ребрами α, β, γ и от соотношения между величинами ребер а, b, с различают семь кристаллографических систем, или сингоний. Каждая из сингоний характеризуется своим соотношением параметров а, b, с и углов α, β, γ , определяемых так, как показано на рис. 1.2. Существуют триклинная, моноклинная, ромбическая, тетрагональная, кубическая, тригональная и гексагональная сингонии. В табл. 1.2 перечислены ячейки, возможные в каждой сингонии, а на рис. 1.6 данные ячейки изображены.
- В триклинной сингонии есть только одна примитивная элементарная ячейка (Р), где атомы находятся лишь в вершинах.
- В моноклинной сингонии есть две элементарных ячейки: примитивная ячейка (Р) и ячейка с центрированными основаниями (С) (непримитивная), где узлы расположены в центрах граней, перпендикулярных оси с.
- В ромбической сингонии есть четыре элементарных ячейки: примитивная ячейка (Р), ячейка с центрированными основаниями (С), объемноцентрированная ячейка (I) и гранецентрированная ячейка (F).
- В тетрагональной сингонии есть две элементарных ячейки: примитивная ячейка (Р) и объемноцентрированная ячейка (I).
- В кубической сингонии возможны три элементарных ячейки: примитивная ячейка (Р) и объемноцентрированная кубическая (I) ячейка, или ОЦК и гранецентрированная кубическая (F) ячейка, или ГЦК. Характеристики трех кубических решеток приведены в таблице 1.3.
- В тригональной сингонии в качестве элементарной ячейки обычно выбирают ромбоэдр. Решетка является примитивной, но обозначают ее буквой R, а не Р.
- В гексагональной сингонии элементарную ячейку выбирают в виде прямой призмы, в основании которой лежит ромб с углом 60о. Для того, чтобы подчеркнуть принадлежность данной ячейки к гексагональной сингонии, часто к ней добавляют еще две ячейки, повернутые друг относительно друга на 120о, получая таким образом утроенную «ячейку» в форме гексагональной призмы (рис. 1.7).
Таблица 1.2
Кристаллографические системы и их характеристики
Кристаллографическая система |
Число ячеек в системе |
Символ ячейки |
Характеристики элементарной ячейки |
Триклинная
Моноклинная
Ромбическая
Тетрагональная
Кубическая
Тригональная
Гексагональная |
1
2
4
2
3
1
1 |
Р
Р, С
Р, С, I, F
P, I
P, I, F
R
P |
а≠b≠с; α≠β≠γ
а≠b≠с; α=γ=β≠90о
а≠b≠с; α=β=γ=90о
а=b≠с; α=β=γ=90о
а=b=с; α=β=γ=90о
а=b=с; α=β=γ<120о≠90о
а=b≠с; α=β=90о, γ=120о |
Следует обратить внимание на то, что если на примитивную элементарную ячейку (Р) приходится один узел, то на элементарную ячейку с центрированными основаниями (С) приходится два узла, на объемноцентрированную элементарную ячейку (I) также приходится два узла, а на гранецентрированную элементарную ячейку (F) приходится четыре узла.
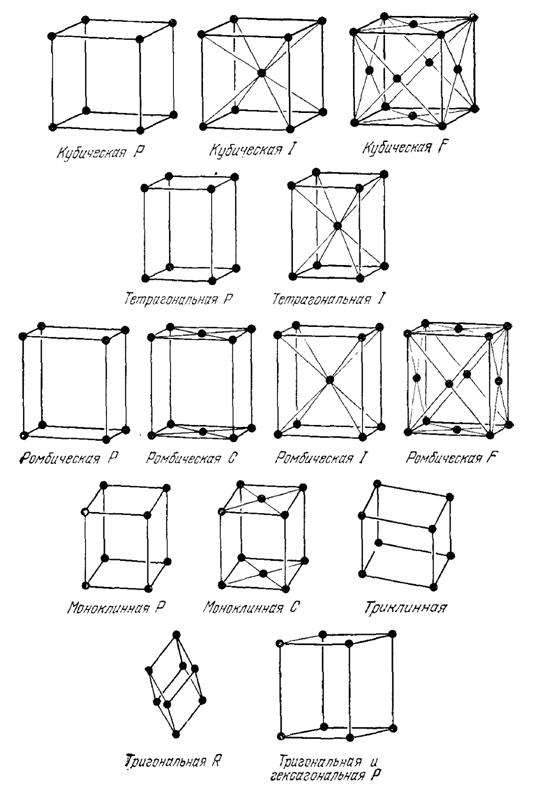
Рис. 1.6. Типы элементарных ячеек, возможных в соответствующих сингониях
Таблица 1.3
Характеристики кубических решеток.
Характеристики |
P |
I |
F |
Объем ячейки |
a3 |
a3 |
a3 |
Число узлов на одну ячейку |
1 |
2 |
4 |
Число узлов на единицу объема |
1/ a3 |
2/ a3 |
4/ a3 |
Расстояние между ближайшими соседями |
a |
a |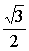
|
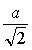
Число ближайших соседей |
6 |
8 |
12 |
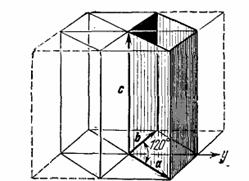
Рис. 1.7. Сопоставление примитивной ячейки гексагональной сингонии (утолщенные линии) и гексагональной призмы. (Здесь a=b≠c).
Таким образом, в этих семи сингониях мы получили 14 типов пространственных решеток – так называемых решеток Браве, которые представляют собой совокупность одинаковых и одинаково расположенных атомов или ионов. Данные атомы (ионы) могут быть совмещены друг с другом путем параллельного переноса. Следует иметь в виду, что кристаллы сложной структуры могут быть представлены как совокупность нескольких решеток Браве, вложенных одна в другую. Это относится как к кристаллам чистых химических элементов, так и к кристаллам сложного химического состава.
|
