1.3. Символы рядов и плоскостей. Индексы Миллера
Ряд, или узловая прямая, характеризуются наклоном в выбранной системе координат. Направление ряда определяется двумя точками – началом координат и любым узлом ряда. Символ этого узла принимают за символ ряда и пишут в квадратных скобках [m n p]. Этот символ характеризует семейство параллельных рядов, а также и параллельные грани кристаллического многогранника. Символы некоторых направлений в плоской сетке показаны на рис. 1.3. Например, ряд [110] можно характеризовать и символом [220], [330] и т. п., но для определения символа ряда принято выбирать узел, ближайший к началу координат. Если индексы в символе ряда кратные, их можно сокращать на целое положительное число. Оси координат OX, OY и OZ имеют соответственно символы [100], [010] и [001].
Положение и ориентация кристаллографических плоскостей определяются заданием координат трех атомов, лежащих в этой плоскости. Удобно, когда каждый из трех атомов лежит на одной из кристаллографических осей координат. Тогда положение плоскости можно задать координатами этих трех атомов по осям в единицах постоянной решетки. Пусть некая плоскость решетки пересекает все три оси координат, отсекая на них отрезки mа, nb, pс (здесь а, b и с – параметры решетки). Отношение чисел m:n:p определяет наклон плоскости (и семейства параллельных ей плоскостей) к осям координат. Например, для семейства плоскостей на рис. 1.4 имеем (табл. 1.1):
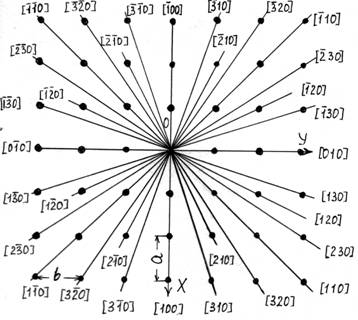
Рис. 1.3. Символы некоторых направлений в плоской сетке
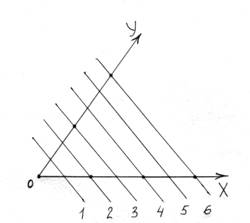
Рис. 1.4. К определению символов семейства параллельных плоскостей
Таблица 1.1
К определению символов семейства параллельных плоскостей
Номер
плоскости |
Отрезки по осям |
m:n:p = p:q:r |
х |
y |
z |
1 |
a/2 |
b/3 |
∞ |
1/2:1/3: ∞ = 3:2: ∞ |
2 |
a |
2b/3 |
∞ |
1:2/3: ∞ = 3:2: ∞ |
3 |
3a/2 |
b |
∞ |
3/2:1: ∞ = 3:2: ∞ |
4 |
2a |
4b/3 |
∞ |
2:4/3: ∞ = 3:2: ∞ |
Серию отношений чисел m:n:p можно представить как отношение взаимно простых чисел p:q:r, так называемых параметров Вейсса (см. таблицу). Плоскости в кристаллографии принято характеризовать индексами Миллера. Индексы Миллера – это величины, обратные параметрам Вейсса, приведенные к целым числам. Если параметры плоскости p, q и r, то индексы Миллера определяются из соотношения:
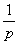 : : 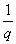 : : 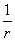 = h:k:l. (1.3) = h:k:l. (1.3)
В приведенном примере (рис. 1.4) h:k:l = 2:3:0.
Числа h, k и l называются индексами плоскости, или индексами Миллера. Символ плоскости имеет обозначение (hkl).
На рис. 1.5 приведены некоторые примеры атомных плоскостей в кубических кристаллах.
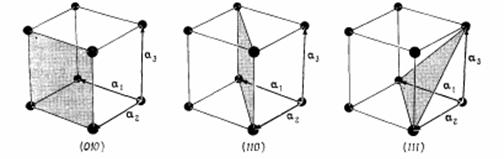
Рис. 1.5. Три атомные плоскости и их индексы Миллера для кубической решетки
Межплоскостное расстояние d для простых прямоугольных решеток находят по формуле:
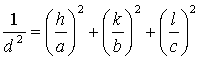 . (1.4) . (1.4)
|