1.2. Основные элементы симметрии кристаллической решетки
Под симметрией кристаллической решетки понимается свойство решетки совпадать с самой собой при некоторых пространственных перемещениях. Кристаллическая решетка может обладать различными видами симметрии.
 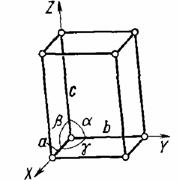
Рис. 1.2. Элементарная ячейка с параметрами a, b, c, α, β, γ, характеризующими пространственную решетку в целом; X, Y, Z – кристаллографическая система координат
Кристаллическое тело, как объект конечных размеров, обладает точечной симметрией – внутри него найдется точка, которая остается на месте – то есть не преобразуется при любом симметричном преобразовании.
Геометрические образы, с помощью которых осуществляются отдельные симметрические преобразования, называют элементами симметрии. Различают такие элементы симметрии, как поворотная ось симметрии (простая и зеркальная), зеркальная плоскость симметрии, центр инверсии.
1. Если решетка совпадает сама с собой при повороте вокруг некоторой оси на угол 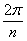 (следовательно, за один полный поворот вокруг оси решетка совпадает сама с собой n раз), то эта ось называется осью симметрии n – го порядка. Возможны только оси симметрии 2, 3, 4 и 6 – го порядков. (следовательно, за один полный поворот вокруг оси решетка совпадает сама с собой n раз), то эта ось называется осью симметрии n – го порядка. Возможны только оси симметрии 2, 3, 4 и 6 – го порядков.
2. Если решетка совпадает сама с собой при зеркальном отражении от некоторых плоскостей, такие плоскости называют плоскостями зеркального отражения.
3. Если кристаллическая решетка в результате операции инверсии 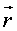 -> - -> - 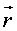 совпадает с исходной ( совпадает с исходной (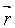 - вектор, определяющий положение произвольной точки кристалла), то она обладает центром инверсии. - вектор, определяющий положение произвольной точки кристалла), то она обладает центром инверсии.
Кроме простых поворотных различают сложные оси симметрии – зеркально поворотные и инверсионные. В первом случае происходит поворот вокруг соответствующей оси и отражение в зеркальной плоскости, во втором – поворот вокруг оси с отражением в центре инверсии.
Но, кроме того, всякая решетка обладает прежде всего трансляционной симметрией – то есть совпадает сама с собой при перемещении (трансляции) на величину периода идентичности. Этот элемент симметрии – трансляция – действует не на какую-то точку решетки, а на всю решетку в целом. При перемещении решетки на трансляцию в направлении вектора трансляции решетка совмещается сама с собой всеми своими точками.
Комбинация трансляции с такими элементами симметрии, как плоскости отражения и оси вращения, дает новые виды элементов симметрии.
1. Поворот около оси симметрии на угол 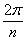 + параллельный перенос на расстояние d вдоль данной оси = винтовая ось, где d должно удовлетворять условию: + параллельный перенос на расстояние d вдоль данной оси = винтовая ось, где d должно удовлетворять условию:
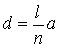 , (1.2) , (1.2)
где l = 1, 2, …, n – 1; a – наименьший период решетки в направлении оси. Так, винтовая ось 2 – го порядка может быть только с одной трансляцией – на половину периода, винтовые оси 3–го порядка связаны с переносом на 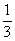 и и 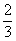 периода. периода.
2. Отражение в плоскости + параллельный перенос вдоль плоскости на расстояние d = плоскость скользящего отражения. Величина d определяется при этом направлением скольжения.
|