1.1 Идеальный кристаллический порядок.
Геометрия кристаллической решетки. Элементарная ячейка
Кристаллические твердые вещества встречаются в природе в виде отдельных одиночных кристаллов – монокристаллов – и в виде поликристаллов, представляющих собой скопления беспорядочно ориентированных мелких кристалликов – кристаллитов.
Особенностью строения кристаллических веществ является наличие так называемого дальнего порядка – корреляции во взаимном расположении атомов (молекул) на расстояниях много больших, чем межатомные. При этом атомы (молекулы) кристалла расположены упорядоченно, образуя симметричный, периодически повторяющийся в пространстве узор, характерный для данного кристалла.
Идентичные точки кристалла (назовем их узлами) образуют трехмерную периодическую решетку, охватывающую все пространство кристалла. Решетку можно описать с помощью периодически повторяющегося в пространстве элементарного параллелепипеда – элементарной ячейки, построенной на трех векторах переноса, или единичных трансляциях 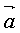 , , 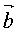 , , 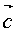 . Эти векторы могут быть выбраны бесчисленным количеством способов, началом трех векторов трансляций можно выбрать любую точку. Если выбрать какой-нибудь узел решетки за начало координат, то любой другой узел решетки определяется радиусом-вектором . Эти векторы могут быть выбраны бесчисленным количеством способов, началом трех векторов трансляций можно выбрать любую точку. Если выбрать какой-нибудь узел решетки за начало координат, то любой другой узел решетки определяется радиусом-вектором 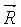 : :
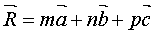 , (1.1) , (1.1)
где m, n, p – числа, которые называют индексами данного узла. Совокупность трех индексов обычно записывают в двойных квадратных скобках [[m n p]] и называют символом узла. На рис.1.1,а показаны символы нескольких узлов в косоугольной плоской сетке (индекс по третьей оси равен нулю), а на рис. 1.1,б символы вершин, центров граней и центра элементарной ячейки, если одна из вершин ячейки принята за начало координат. Например, узел в центре куба имеет символ [[ 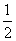 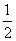 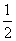 ]], узлы в центрах граней – символы [[ ]], узлы в центрах граней – символы [[ 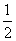 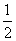 0 ]], [[ 0 0 ]], [[ 0 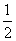 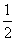 ]] и [[ ]] и [[ 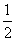 0 0 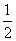 ]]. ]].
Обычно векторы трансляций выбирают в качестве ортов системы координат, связанной с кристаллографическими осями. Элементарная ячейка в общем случае представляет собой косоугольный параллелепипед с ребрами 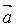 , , 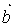 , , 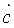 и углами α, β и γ (рис. 1.2); α – угол между осями Y и Z, β – между осями X и Z, γ – между осями X и Y. Шесть указанных величин называют параметрами решетки. и углами α, β и γ (рис. 1.2); α – угол между осями Y и Z, β – между осями X и Z, γ – между осями X и Y. Шесть указанных величин называют параметрами решетки.
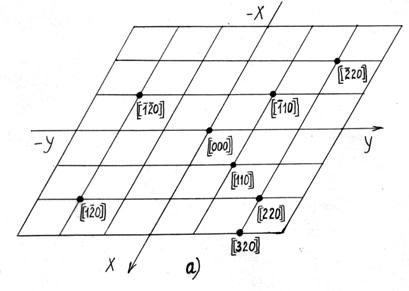
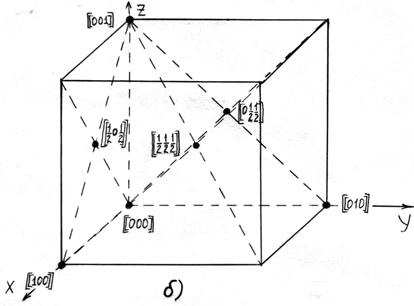
Рис. 1.1. Символы узлов в плоской сетке (а) и вершин центра куба и центров граней куба (б)
Элементарный параллелепипед, построенный на кратчайших трансляциях a, b и c, является основным параллелепипедом решетки. Такой параллелепипед не содержит дополнительных узлов ни в какой точке внутри или на поверхности, кроме вершин, и его называют примитивным, или примитивной элементарной ячейкой.
|