3. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДЫХ ТЕЛ
- Момент инерции материальной точки
где 
— масса точки; 
— расстояние от точки до оси вращения.
- Моменты инерции тел правильной геометрической формы (тела считаются однородными;
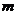— масса тела) представлены в таблице:
Тело |
Положение оси вращения |
Момент инерции |
Полый тонкостенный цилиндр или кольцо радиусом R |
Ось симметрии |
|
Сплошной цилиндр или диск радиусом R |
Ось симметрии |
|
Прямой тонкий стержень длиной l |
Ось перпендикулярна стержню и проходит через его середину |
|
Прямой тонкий стержень длиной l |
Ось перпендикулярна стержню и проходит через его конец |
|
Шар радиусом R |
Ось проходит через центр шара |
|
- Теорема Штейнера
где 
- момент инерции тела относительно оси, проходящей через центр масс; 
– момент инерции относительно параллельной оси, отстоящей от первой на расстоянии 
;
– масса тела.
Пример: Найти момент инерции шара относительно оси 
, находящейся на расстоянии 
от поверхности шара (рис.4).
Здесь
; 
.
Следовательно,
.
Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,
где 
- момент инерции тела относительно оси 
; 
- его угловая скорость.
- Кинетическая энергия тела, катящегося по плоскости без скольжения,
где 
– масса тела; 
– скорость центра масс тела; 
– момент инерции тела относительно оси, проходящей через его центр масс; 
- угловая скорость тела.
- Момент силы относительно неподвижной точки
где 
- радиус-вектор, проведенный из этой точки в точку приложения силы 
. Модуль момента силы относительно неподвижной оси
,
где 
– плечо силы (кратчайшее расстояние между линией действия силы и осью вращения), 
– угол между направлениями силы и радиуса-вектора. Направление момента силы совпадает с осью, относительно которой происходит вращение, и может быть определено по правилу буравчика.
- Работа при вращении тела
где 
– угол поворота тела; 
– момент силы относительно оси 
.
- Момент импульса (момент количества движения) твердого тела (рис. 5) относительно оси вращения
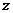
- где
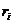– расстояние от оси 
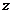до отдельной частицы тела; 
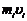– импульс этой частицы; 
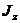– момент инерции тела относительно оси 
; 
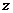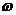– его угловая скорость.
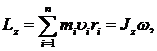
Рис.5
- Уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси
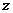
где 
– угловое ускорение; 
– момент инерции тела относительно оси 
.
- Закон сохранения момента импульса для замкнутой системы тел
Пример: Платформа в форме диска массой 
и радиусом 
вращается относительно вертикальной оси, проходящей через ось симметрии. На краю платформы стоит человек массой 
(рис. 6). Как изменится угловая скорость вращения, если человек перейдёт на расстояние 
ближе к оси (рис. 7) (человека считать материальной точкой)?
Рис . 6 Рис. 7
По закону сохранения момента импульса
,
где 
и 
- моменты инерции платформы с человеком, т.е.
; 
Получаем:
