5. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ
ИДЕАЛЬНОГО ГАЗА
Основное уравнение молекулярно-кинетической теории:
где 
– давление газа; 
– концентрация молекул; 
– общее число молекул; 
– объём; 
– масса одной молекулы; 
– средняя квадратичная скорость одной молекулы; 
– плотность газа; 
- масса газа; 
– абсолютная температура; 
– постоянная Больцмана.
- Средняя кинетическая энергия поступательного движения одной молекулы
,
где 
– число степеней свободы [для одноатомной молекулы 
поступательным степеням; для двухатомной молекулы 
(3 поступательные и 2 вращательные); для трёхатомной молекулы 
(3 поступательные и 3 вращательные)].
- Изопроцессы (газовые законы) – для
:
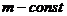1)
- изотермический:
(рис.8, а, б, в)
2)
- изобарный:
(рис. 9, а, б, в)
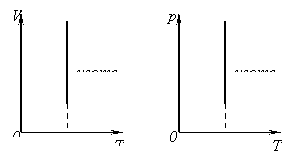
3)- изохорный:
(рис.10, а, б, в)
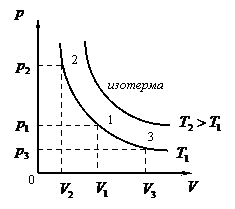
а)
б) в)
;
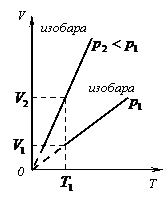
а)
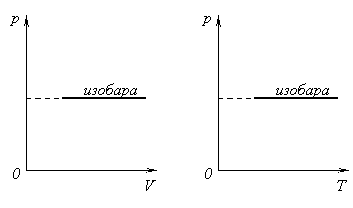
б) в)
Рис.9.
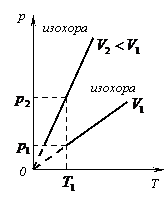
а)
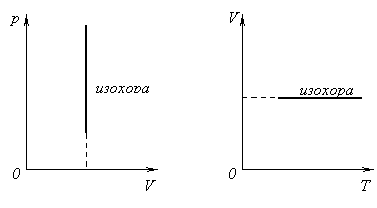
б) в)
Рис.10.
- Уравнение Менделеева-Клапейрона:
,
где 
– объём газа; 
– масса газа; 
– молярная масса; 
– универсальная газовая постоянная.
- Количество вещества (число молей):
,
где 
– общее число молекул; 
– постоянная Авогадро.
- Масса одной молекулы:
.
- Скорости молекул:
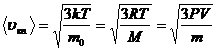– средняя квадратичная;
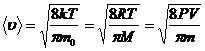– средняя арифметическая;
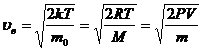– наиболее вероятная.
- Закон Максвелла для распределения молекул идеального газа по скоростям:
,
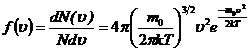где функция 
распределения молекул по скоростям определяет относительное число молекул 
из общего числа Nмолекул, скорости которых лежат в интервале от 
до 
.
Из этой формулы следует, что
~
~
~
,
где 
- масса одной молекулы; 
- молярная масса; 
- масса газа.
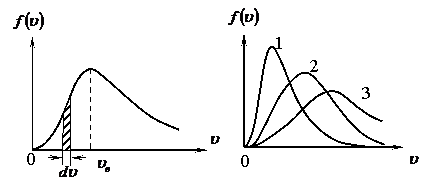
Рис.11. Рис.12
На рис.11 площадь заштрихованной полоски равна относительному числу молекул, скорости которых лежат в интервале от 
до 
.
Графики на рис.12 соответствуют (при прочих равных параметрах):
или 
.