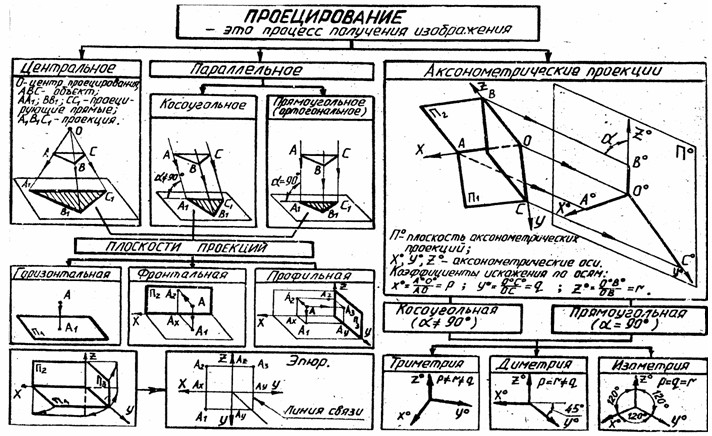
§3. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ.
На рис.28 изображены ортогональные и аксонометрическая проекции предмета.
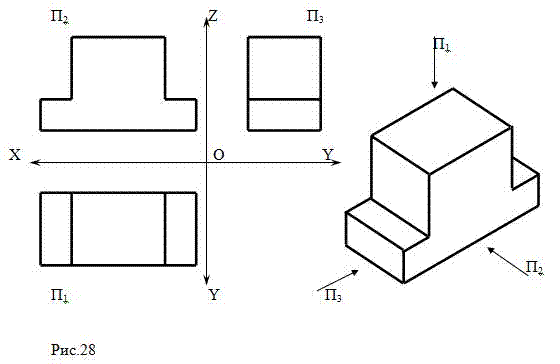
Каждая ортогональная проекция предмета показывает его форму только с одной стороны: фронтальная то, что мы
видим спереди, горизонтальная – сверху, профильная – слева. Представить форму предмета только по ортогональным проекциям иногда трудно.
Поэтому используют аксонометрические проекции. С их помощью можно получить изображение, на котором форма предмета будет
видна с трех сторон одновременно. Аксонометрические проекции часто используются в техническом черчении. Они характеризуются
наглядностью и простотой построения.
Для получения аксонометрических проекций используют метод параллельного проецирования. Предмет вместе с осями
прямоугольных координат Х, Y, Z параллельными лучами проецируют на дополнительную плоскость П0 (Рис.29).
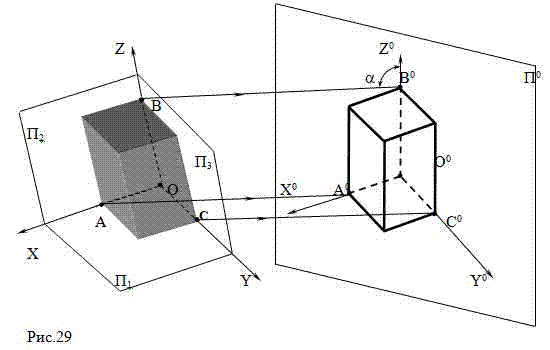
ЗАПОМНИТЕ Аксонометрической проекцией или аксонометрией называется изображение, которое получается
при параллельном проецировании предмета вместе с осями прямоугольных координат на плоскость.
Плоскость П0, на которой построено изображение предмета, называется плоскостью аксонометрических проекций. Изображение предмета на
плоскости П0 называется аксонометрической проекцией или аксонометрией. Проекции прямоугольных осей координат Х,Y,Z на плоскости
П0 – прямые X0, Y0, Z0 называются аксонометрическими осями.
1. Виды аксонометрических проекций.
При построении аксонометрии отрезки осей координат проецируются на плоскость П0 с искажением.
Искажаются и размеры предметов, которые изображаются в аксонометрии. Искажение линейных размеров характеризуется коэффициентами
искажения по осям. Коэффициенты искажения обозначают и определяют так:
Величина коэффициента искажения зависит от взаимного расположения (углов наклона) осей координат Х,Y,Z
и плоскости аксонометрических проекций П0. Если все коэффициенты искажения различны, то есть, p#g#r,то аксонометрия называется триметрией.
Если равны коэффициенты искажения только по двум осям, то есть p=g#r или p#g=r, или p=r#g, то проекции называются диметрией. Аксонометрические проекции
называются изометрией, если коэффициенты искажения по всем осям равны, то есть p=g=r.
Изометрия, диметрия и триметрия могут быть прямоугольными и косоугольными, так как проецирующие лучи имеют угол
наклона a с плоскостью П0. Если a=900, то аксонометрические проекции прямоугольные, если a#900 - косоугольные.
В данном пособии рассматривается построение прямоугольной изометрической проекции, которую мы будем называть
изометрия.
В изометрии углы между всеми осями равны 1200 (Рис.30). Ось Z0 располагается вертикально,
оси Х0 и Y0 могут быть направлены как вверх, так и вниз.
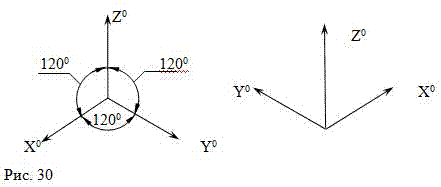
ВНИМАНИЕ! Изометрические оси под углом 1200 можно построить с помощью (Рис.31):
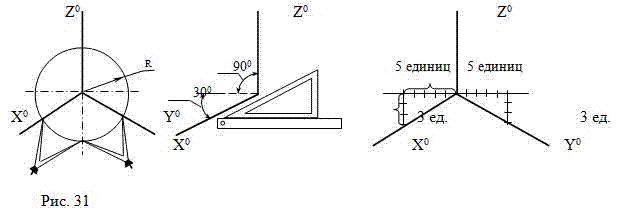
а)циркуля, разделив любую
окружность на три равные части; | б)угольника с углами
300, 600, 900; | в)отношения 5:3 катетов
прямо-угольного треуголь-ника. |
Коэффициенты искажения в прямоугольной изометрии равны:p=g=r=0,82.
Для простоты построений изометрию выполняют без искажения по осям, то есть принимают, что коэффициенты искажения равны единице (p=g=r=1).
Таким образом, изображение в изометрии увеличивается в 1/0,82=1,22 раза.
2. Изометрия точки.
Изометрию точки, а также любого предмета, строят по их заданным ортогональным проекциям.
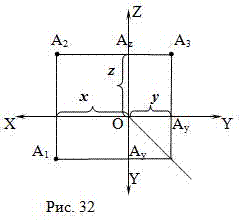
На рис.32 даны ортогональные проекции точки А. Построим изометрию точки А (Рис.33):
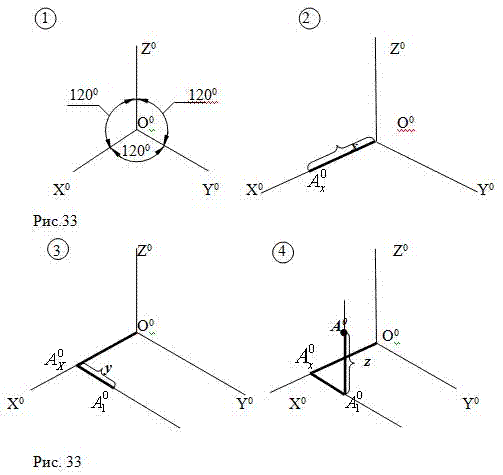
1)в произвольной точке 00 проведем изометрические оси Х0, Y0,Z0;
2)от точки 00 по оси Х0 отложим расстояние 0Аx (координата Х точки А), отметим точку;
A0x
3)из точки A0x проведем прямую параллельную оси Y0 и по ней отложим
расстояние АxА1(координату Y точки А), отметим точку A01;
4) из точки A01 проведем прямую, параллельную оси Z0 и по ней
отложим расстояние ОАz (координата точки А),отметим точку А0 – изометрию точки А.
Ломаная линия O0 A0x A01 A0
называется координатной ломанной.
ЗАПОМНИТЕ!Чтобы построить изометрию точки, надо построить координатную ломаную этой точки в системе изометрических осей.
Аналогично изометрию точки можно построить по ее координатам.
Задача 1. Задана точка В (40;0;30). Построить изометрию точки В (Рис.34):
1)от точки 00по оси Х0 отложим 40 мм (координата Х точки В), отметим точку B0x;
2)координата Y точки В равна нулю, поэтому B01=B0x;
3)из точки B01 параллельно оси Z проведем прямую и по ней отложим 30 мм (координата Z точки В),
отметим ВB0 – изометрию точки В.
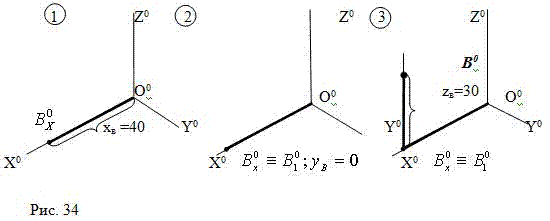
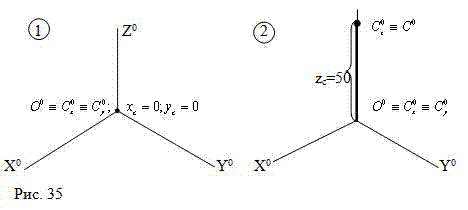
Задача 2. Задана точка С (0;0;50). Построить изометрию точки С (Рис. 35):
1)координата Х и Y точки С равны нулю, поэтому 0=C0x=C0y;
2)из точки 0 по оси Z0 отложим 50 мм (координата точки С) и отметим точку С0 – изометрию точки С.
ВНИМАНИЕ! Координатная ломаная точек частного положения состоит из:
- двух отрезков, если одна координата точки равна нулю, и точка расположена на плоскости;
- одного отрезка, если две координаты точки равны нулю, и точка расположена на оси.
Структурно-логические схемы §§ 1,2,3 даны на стр. 23-24.
Словарный минимум:
аксонометрия | представлять (что?) |
наглядность | искажать (что?) |
триметрия | |
диметрия | |
изометрия | |
ЗАДАНИЯ.
1.Ответьте на вопросы.
1.Что называется аксонометрической проекцией?
2.В чем различие между прямоугольными и косоугольными аксонометрическими проекциями?
3.Какие аксонометрические проекции называются изометрическими, а какие – диметрическими?
4.Каковы углы между осями в прямоугольной изометрии и коэффициенты искажения по осям?
5.Что нужно построить, чтобы найти аксонометрию точки?
6.Сколько отрезков составляют координатную ломаную точки общего положения? Почему?
7.Сколько отрезков составляют координатную ломаную точки, которая расположена на оси? Почему?
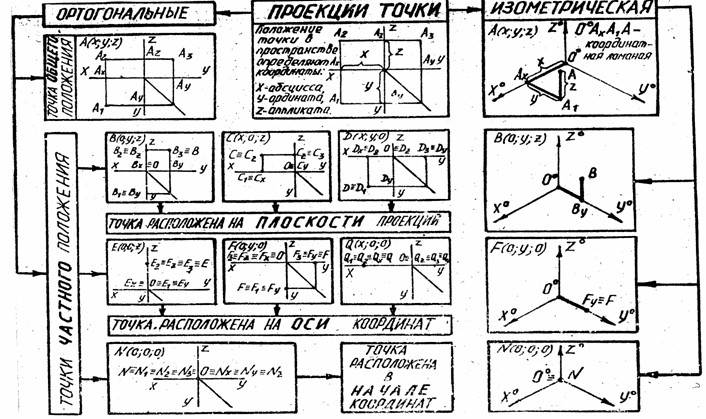
2.Выполнение в тетради упражнения:
1.По заданным проекциям точки постройте эпюр и изометрию точки:
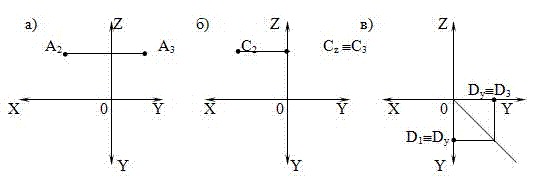
Ответьте на вопросы: 1. Где расположена точка?
2. Как она называется?
2.Точка задана координатами. Постройте эпюр и прямоугольную изометрию точки:
а) В (35;0;20); | б) С (40;20;20); | в) F (30;20;0); |
г) D (0;25;20); | д) M (0;30;0); | е) L (40;0;0). |
3. Выполните тестовые задания с выбором правильного ответа.
Тест №1.

1.Точка А является точкой общего положения на рисунке…
a) 1; | c) 3; | e) такого рисунка нет. |
b) 2; | d) 4; | |
2.Точка А принадлежит фронтальной плоскости проекций на рисунке …
a) 1; | c) 3; | e) такого рисунка нет. |
b) 2; | d) 4; | |
3.Точка А принадлежит горизонтальной плоскости проекций на рисунке …
a) 1; | c) 3; | e) такого рисунка нет. |
b) 2; | d) 4; | |
4.Точка А принадлежит профильной плоскости проекций на рисунке …
a) 1; | c) 3; | e) такого рисунка нет. |
b) 2; | d) 4; | |
5.Точка А принадлежит оси проекций OX на рисунке …
a) 1; | c) 3; | e) такого рисунка нет. |
b) 2; | d) 4; | |
6.Точка А принадлежит оси проекций OY на рисунке …
a) 1; | c) 3; | e) такого рисунка нет. |
b) 2; | d) 4; | |
7.Точка А максимально удалена от горизонтальной плоскости проекций на рисунке…
a) 1; | c) 3; | e) такого рисунка нет. |
b) 2; | d) 4; | |
8.Точка А максимально удалена от профильной плоскости проекций на рисунке …
a) 1; | c) 3; | e) такого рисунка нет. |
b) 2; | d) 4; | |
9.Точка А максимально удалена от фронтальной плоскости проекций на рисунке …
a) 1; | c) 3; | e) такого рисунка нет. |
b) 2; | d) 4; | |
10.Точка А одинаково удалена от горизонтальной и профильной плоскости проекций на рисунке…
a) 1; | c) 3; | e) такого рисунка нет. |
b) 2; | d) 4; | |
Тест №2.

1.Плоскость проекций, которой принадлежит точка C …
a) горизонтальная; | c) профильная; |
b) фронтальная; | d) точка находится в пространстве. | |
2.Плоскость проекций, которой принадлежит точка D …
a) горизонтальная; | c) профильная; |
b) фронтальная; | d) точка находится в пространстве. | |
3.Плоскость проекций, которой принадлежит точка E …
a) горизонтальная; | c) профильная; |
b) фронтальная; | d) точка находится в пространстве. | |
4.Координата точки E, которая равна нулю …
a) X; | c) Z; |
b) Y; | d) такой координаты нет. | |
5.Координата точки B, которая равна нулю …
a) X; | c) X и Z; |
b) X и Y; | d) такой координаты нет. | |
6.Координата точки C, которая равна нулю …
a) X; | c) Z; |
b) Y; | d) такой координаты нет. | |
7.Максимальная координата точки D …
a) X; | c) Z; |
b) Y; | d) такой координаты нет. | |
8.Точки, которые одинаково удалены от фронтальной плоскости проекций …
a) C, D; | c) B,D; |
b) Е, D; | d) таких точек нет. | |
9. Точка, максимально удаленная от горизонтальной плоскости проекций …
10. Точка, одинаково удаленная от фронтальной и профильной плоскостей проекций …
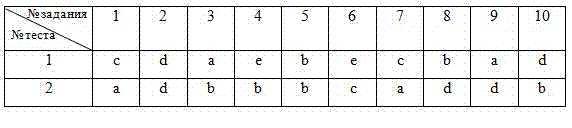
Ответы к тестам.
|
