ЗАПОМНИТЕ! Ортогональная проекция точки – это точка пересечения перпендикуляра, который проходит через данную точку, с плоскостью проекций.

Рассмотрим обратную задачу. Известна A₁ – ортогональная проекция точки А на плоскость П₁. Определим положение точки А в пространстве (Рис.8). Для этого через точку A₁ проведем перпендикуляр к плоскости П₁. Проекция A₁ будет соответствовать любой точке ( и т.д.), которая находится на перпендикуляре. Поэтому мы не можем определить положение точки А в пространстве (Рис.9).

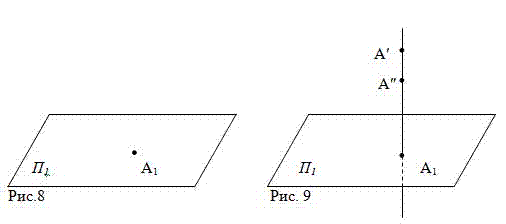
ЗАПОМНИТЕ! Одна проекция точки не определяет положение точки в пространстве.

2. Проекции точки на двух плоскостях проекций.

Определить положение точки в пространстве можно, если проецировать точку не на одну, а на две взаимно перпендикулярные плоскости проецирующими прямыми, которые перпендикулярны этим плоскостям проекций.

В пространстве даны точка А и две взаимно перпендикулярные плоскости П₁ и П₂ (Рис.10). Найдем проекции точки А на плоскости П₁ и П₂. Для этого из точки А опустим перпендикуляр на плоскость П₁ и отметим А₁ – проекцию точки А на плоскость П₁ (Рис.11). Затем из точки А опустим перпендикуляр на плоскость П₂ и отметим точку А₂ – проекцию точки А на плоскость П₂ (Рис.12).

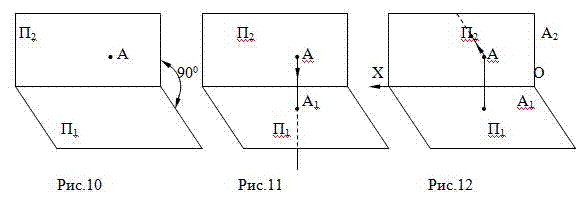
ЗАПОМНИТЕ! Две проекции точки определяют положение точки в пространстве.

3. Проекции точки на трех плоскостях проекций.

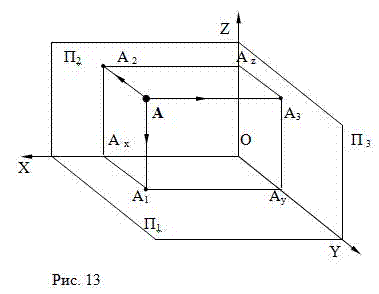
При изображении более сложных, чем точка предметов, строят их третью проекцию. Для этого используют еще одну плоскость проекций П₃, которая перпендикулярна плоскостям П₁ и П₂ (Рис.13). Чтобы построить проекцию точки А на плоскость П₃, из точки А опустим перпендикуляр на плоскость П₃ и отметим точку А₃ – проекцию точки А на плоскость П₃.

Плоскости проекций будем называть:

П₁ – горизонтальная плоскость проекций;

П₂ – фронтальная плоскость проекций;

П₃ – профильная плоскость проекций.

Аналогично проекции точки А называются: А₁ – горизонтальная, А₂ – фронтальная, А₃ – профильная. Линии пересечения плоскостей проекций называются осями проекций или осями координат:

ось ОХ – линия пересечения плоскостей проекций П₁ и П₂;

ось ОY – линия пересечения плоскостей проекций П₁ и П₃;

ось ОZ – линия пересечения плоскостей проекций П₂ и П₃;

Точка О – точка пересечения осей проекций (координат) X, Y, Z называется началом координат.

Перпендикуляры из проекций А₁ и А₂ на ось ОХ пересекаются в одной точке. Ее обозначают А_х. А_у – точка пересечения перпендикуляров из проекций А₁ и А₃ на ось OY. А_z – точка пересечения перпендикуляров из проекций A₂ и A₃ на ось ОZ. Прямые A₁A_x, A₂A_x, A₂A_y, A₃A_z, A₁A_y, A₃A_y, которые соединяют проекции точки, называются линиями связи.

4. Эпюр точки.

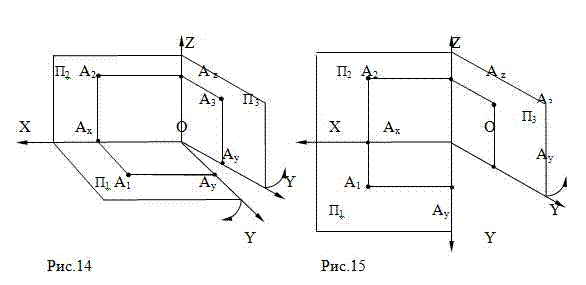
Проекциями, которые построены на трех взаимно перпендикулярных плоскостях, пользоваться неудобно, так как их надо чертить на бумаге, которая представляет собой плоскость. Поэтому взаимно перпендикулярные плоскости проекций совмещают в одну плоскость путем их поворота вокруг осей проекций. Для этого мысленно разделим плоскости П₁ и П₃ по оси ОY (Рис.14). Плоскость П₂ остается неподвижной. Плоскость П₁ повернем вокруг оси ОХ до ее совмещения с плоскостью П₂ (Рис.15). 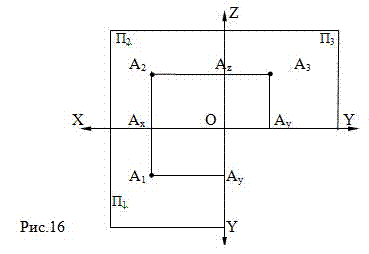Плоскость П₃ повернем вокруг оси ОZ до совмещения с плоскостью П₂ (Рис.16). Таким образом, мы получили чертеж, на котором изображены ортогональные проекции точки, которые расположены в проекционной связи, то есть, соединены между собой линиями связи. Этот чертеж называется эпюром (Рис.17).

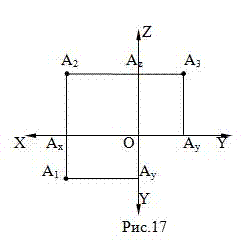
ЗАПОМНИТЕ! На эпюре (Рис.17): 1)границы плоскостей проекций не показывают;

2)ось ОY и все точки, которые на ней расположены, изображают два раза;

3)горизонтальная и фронтальная проекции точки расположены на перпендикуляре к оси ОХ, фронтальная и профильная – на перпендикуляре к оси OZ;

4)изображены только проекции точки, самой точки нет.

Если заданы две любые проекции точки, то можно построить ее третью проекцию.

Задача 1. По заданным горизонтальной и фронтальной проекциям точки С построить ее профильную проекцию (Рис. 18). Для этого:

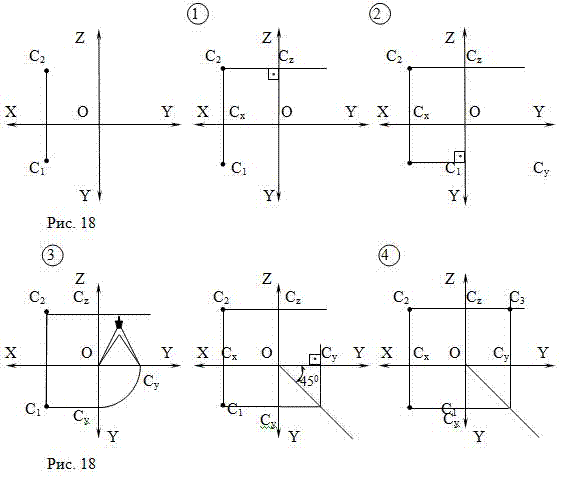
1) через точку C₂ перпендикулярно оси OZ проведем линию связи C₂C_z;

2) через точку C₁ проведем перпендикулярно оси ОY линию связи C₁C_y;

3) расстояние OC_y отмерим по горизонтальной оси OY с помощью дуги окружности или с помощью прямой, проведенной через точку O под углом 450 к осям OY (эта прямая называется постоянной прямой чертежа); для этого линию связи C₁C_y продолжим до пересечения с прямой, а затем из точки пересечения проведем перпендикуляр к горизонтальной оси OY;

4) продолжим линию связи из точки C_y до пересечения с линией связи C₂C_z , получим C₃ – профильную проекцию точки С.

Задача 2. По фронтальной и профильной проекциям точки В построить ее горизонтальную проекцию (Рис.19).

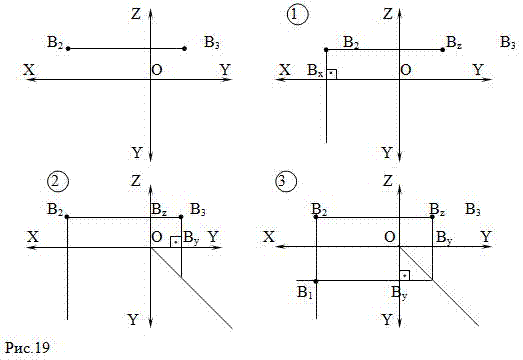
1)из точки B₂ перпендикулярно оси ОХ проведем линию связи B₂B_x;

2)из точки B₃ перпендикулярно горизонтальной оси ОY проведем линию связи B₃B_y до пересечения с постоянной прямой чертежа;

3)из этой точки перпендикулярно вертикальной оси ОY проведем линию связи до пересечения с линией связи B₂B_x. Получим B₁ – горизонтальную проекцию точки В.

Задача 3. По заданным горизонтальной и профильной проекциям точки Е построить ее фронтальную проекцию (Рис.20).

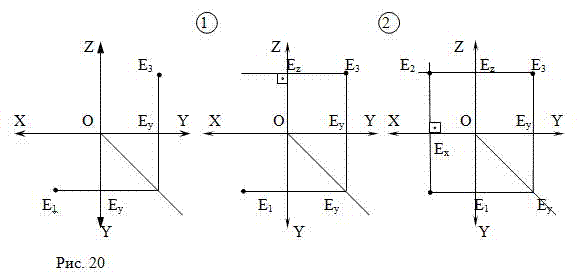
1)из точки E₃ перпендикулярно оси ОZ проводим линию связи E₃E_z ;

2)из точки E₁ перпендикулярно оси ОХ проводим линию связи E₁E_x до пересечения с линией связи E₃E_z. Получим E₂ – фронтальную проекцию точки Е.

ЗАПОМНИТЕ! По двум проекциям точки можно построить ее третью проекцию.

5. Координаты точки.

Положение точки в пространстве можно задавать не только графически в виде эпюра, но и числами, которые определяют расстояния от точки до плоскостей проекций.

ЗАПОМНИТЕ! Расстояние от точки до плоскости проекций называется координатой.

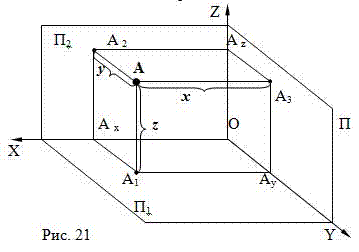
Расстояние от точки до плоскости П₃ определяют координатой Х, она называ-ется абсциссой (Рис.21).

X=A A₃= A₂ A_z= A₁ A_y= A_x0

Расстояние от точки до плоскости П₂ – координатой Y, она называ-ется ординатой.

Y=A A₂= A₁ A_x= A₃ A_z= A_y0

Расстояние от точки до плоскости П₁ - координатой Z , она называется аппликатой.

X=A A₁= A₂ A_x= A₃ A_y= A_z0

ЗАПОМНИТЕ! Координаты измеряются по осям OX, OY, OZ или по линиям, которые параллельны этим осям.

Координаты пишут в скобках рядом с обозначением точки. На первом месте стоит координата Х, на втором – Y, на третьем -Z. Например, запись

А (10;30;20) означает, что координаты точки А такие: Х=10 единиц, Y=30 единиц,Z=20 единиц.

По трем координатам точки можно построить ее эпюр и определить положение в пространстве.

Задача 1. Задана точка А (30;20;50). Построить эпюр точки и определить ее положение в пространстве (Рис.22).

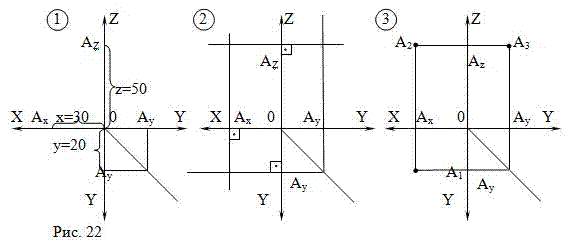
ВНИМАНИЕ! За единицу длины при выборе масштаба принимаем 1 мм, так как в техническом черчении все размеры измеряются в миллиметрах.

1) от точки O по оси OХ откладываем 30 мм, отметим Ах; от точки O по оси OY откладываем 20 мм, отметим Ау; от точки O по оси OZ откладываем 50 мм, отметим А ;

2) через точку A_x проведем перпендикуляр к оси OХ, через А проведем перпендикуляр к оси OZ, через A_y проведем перпендикуляры к осям OY;

3) отметим точки пересечения перпендикуляров: A₁ – горизонтальная проекция, точка пересечения перпендикуляров к осям OХ и OY; A₂ – фронтальная проекция, точка пересечения перпендикуляров к осям OХ и OZ; A₃ – профильная проекция, точка пересечения перпендикуляров к осям OY и OZ.

ЗАПОМНИТЕ! Если ни одна координата точки не равна нулю, она называется точкой общего положения и расположена в пространстве.

4) так как ни одна координата точки А не равна нулю, точка A является точкой общего положения и расположена в пространстве; на эпюре она не изображена.

Задача 2. Задана точка С (40;0;30). Построить эпюр точки С и определить ее положение в пространстве (Рис.23).

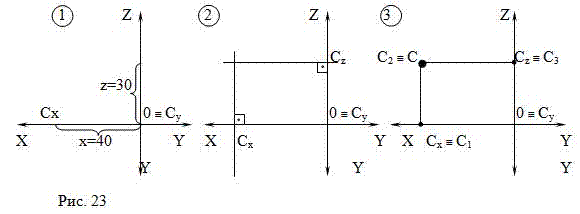
1) от точки O по оси Х откладываем 40 мм, отметим C_x; от точки O по оси OY откладываем 0 мм, следовательно C_y совпадает с точкой O; от точки O по оси OZ откладываем 30 мм, отметим С .

ВНИМАНИЕ! Слово совпадает обозначают знаком и записывают 0 C_y (0 совпадает с C_y).

2) через C_x проведем перпендикуляр к оси OХ, через C_z проведем перпендикуляр к оси OZ; перпендикуляр через C_y совпадает с осью OZ;

3) отметим точки пересечения перпендикуляров: C₂ – фронтальная проекция, точка пересечения перпендикуляров к осям OХ и OZ; C₁ – горизонтальная проекция, совпадает с C_x (C1?CX), т.к. перпендикуляр, который проведен через C_y к вертикальной оси OY, пересекается с перпендикуляром, который проведен через C_x к оси OХ, в точке C_x; C₃ – профильная проекция, совпадает с C_z (C3?CZ), т.к. перпендикуляр, который проведен через C_y к горизонтальной оси OY, пересекается с перпендикуляром, который проведен через C_z к оси OZ, в точке C_z;

ЗАПОМНИТЕ! Если хотя бы одна координата точки равна нулю, точка называется точкой частного положения.

4) координата Y точки С равна нулю, то есть расстояние от точки С до плоскости П₂ равно нулю, следовательно, точка С лежит на плоскости П₂ и совпадает со своей фронтальной проекцией (C ? C2); таким образом, точка С является точкой частного положения и расположена на фронтальной плоскости проекций; на эпюре она совпадает со своей фронтальной проекцией.

ЗАПОМНИТЕ! Если одна координата точки равна нулю, то точка расположена на плоскости проекций и две проекции этой точки лежат на осях проекций, третья – лежит на плоскости и совпадает с точкой (Рис.24).

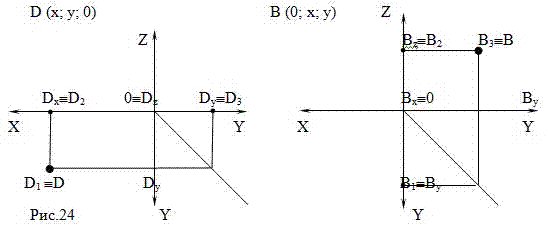
Задача 3. Задана точка Е (0;0;50). Построим эпюр точки и определим ее положение в пространстве (Рис.25).

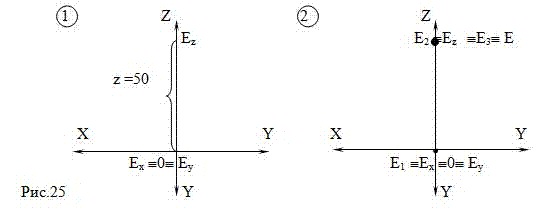
1)Ex?Ey ?0, так как х=0 и у=0; от точки O по оси OZ откладываем 50 мм, отметим E_z;

2)координаты Х и Y точки Е равны нулю, то есть расстояние от точки Е до плоскостей проекций П₂ и П₃ равны нулю, следовательно, точка Е лежит на оси OZ и совпадает со своими фронтальной и профильной проекциями (E?E2?E3); таким образом, точка Е является точкой частного положения и расположена на оси OZ.

ЗАПОМНИТЕ! Если две координаты точки равны нулю, то точка расположена на оси проекций, две ее проекции совпадают и лежат на этой же оси, а третья – в начале координат (Рис.26).

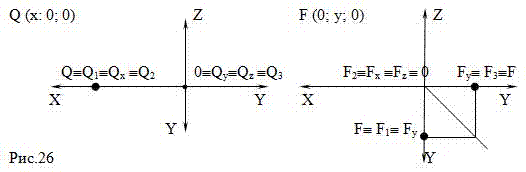
ЗАПОМНИТЕ! Если три координаты точки равны нулю, то точка лежит в начале координат, все проекции точки совпадают и лежат в начале координат (Рис.27).

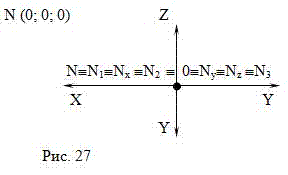
Словарный минимум:

совокупность	соответствовать (чему?)	фронтальный
связь	совмещать (что?; с чем?)	профильный
поворот	совпадать (с чем?)	общий
эпюр		частный
координата

ЗАДАНИЯ.

1.Ответьте на вопросы.

1.Что называется проекцией точки?

2.Сколько проекций определяют положение точки в пространстве?

3.Сколько и какие плоскости проекций вы знаете? Как их обозначают? Как они расположены относительно друг друга?

4.Как образуются оси проекций? Как их обозначают?

5.Что называется линией связи?

6.Что такое эпюр?

7.Что называется координатой точки?

8.Какая точка называется точкой общего положения?

9.Какая точка называется точкой частного положения?

10.Где будут расположены горизонтальная, фронтальная и профильная проекции точки, которая лежит на фронтальной плоскости проекций?

11.Где будут расположены проекции точки, которая лежит на оси OY?

2.Выполните в тетради упражнения.

1.По двум заданным проекциям точки постройте ее третью проекцию и определите положение точки в пространстве:

2.По эпюру точки определите ее координаты:.

3.По координатам точки постройте ее эпюр. Определите положение точки в пространстве:

a) F (50; 0; 30); б) С (40; 50; 10); в) N (0; 50; 0); г) Q (0; 0; 0).