

|
Пересечение двух плоскостей Две плоскости пересекаются по прямой линии. Для построения линии их пересечения необходимо найти две точки, принадлежащие этой линии. Задача упрощается, если одна из пересекающихся плоскостей занимает частное положение. В этом случае ее вырожденная проекция включает в себя проекцию линии пересечения плоскостей. 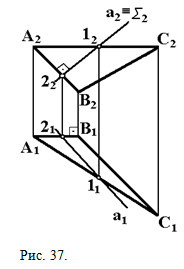
На рис. 37 приведен комплексный чертеж двух пересекающихся плоскостей: плоскости треугольника АВС и Σ, причем Σ плоскость частного положения - фронтально проецирующая. Она пересекает линии АВ и АС плоскости, заданной треугольником ABC , которая является плоскостью общего положения. Точки пересечения 1 и 2 и определяют линию пересечения плоскостей. Соединив их, получаем искомую линию. Линию пересечения двух плоскостей, занимающих общее положение, можно построить в исходной системе плоскостей проекций. Для этого дважды решают задачу на построение прямой пересечения одной плоскости со второй плоскостью. Задачу можно решать в новой системе плоскостей проекций, построив изображение одной из пересекающихся плоскостей как плоскости проецирующей. На рис. 38 построена линия пересечения двух треугольников ABC и DEF путем построения точки М пересечения линии АВ с плоскостью DEF и точки N пересечения линии EF с плоскостью АВС: 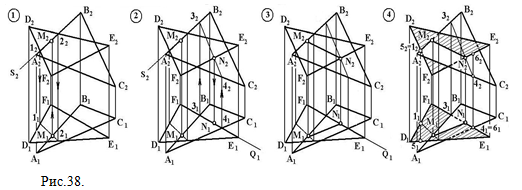 Рис.38.
Рис.38.
1) Через линию АВ проводим фронтально проецирующую плоскость S (S_|_П2 ← S2 ≡А2В2). Тогда S2 пересекает плоскость DEF в точках 1 и 2. Соединим проекции точек 12-22 и 11-21, 11-21 пересекает А1B1 в точке М1. Проводим линию связи M1M2 || А1A2, М1М2 пересекает А2В2 в точке М2. Точка М (М1;М2) - точка пересечения линии АВ с плоскостью DEF. 2) Через EF проводим горизонтально проецирующую плоскость Q (Q _|_П1← Q1 ≡ E1F1), Q 1пересекает ABC в точках 3 и 4. Соединим проекции точек 32-42 и 31-41, 32-42 пересекает E2F2 в точке N2. Проводим линию связи N1N2 || A1A2; N1N2 пересекает E1F1 в точке N1. Точка N (N1;N2) – точка пересечения линии EF с плоскостью АВС. 3) Соединим проекции точек M1 и N1, M2 и N2 получим проекции отрезка MN , который является линией пересечения плоскостей ABC и DEF. 4)После построения определяем видимость пересекающихся плоскостей. На фронтальной плоскости она определена с помощью фронтально конкурирующих точек 1 и 5. Для определения видимости на горизонтальной плоскости проекций использованы горизонтально конкурирующие точки 4 и 6. На рис. 39 эта же линия пересечения построена с помощью дополнительных проекций данных плоскостей на плоскости П4, относительно которой плоскость DEF занимает проецирующее положение. Дополнительные проекции построены из условия, что горизонталь h ∈ DEF проецируется в точку на плоскости П4 _|_ h. Новые линии связи проведены через незаменяемые горизонтальные проекции точек А, В, С, D, E, F параллельно h1 , а новая ось 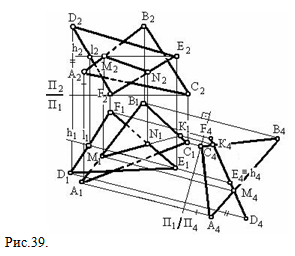
проекций П1/П4 _|_ h1. Замеренные на плоскости П2 высоты точек определили их проекции на плоскости П4. Проекции плоскостей A4B4C4 и D4E4F4 пересекаются по отрезку прямой M4K4, так как А4В4 пересекается с D4E4F4 в М4, а В4С4 пересекается с D4E4F4 в К4. По направлению новых линий связи определяем горизонтальную проекцию линии МК (М1К1). Отмечаем точку пересечения стороны EF c линией МК: E1F1 пересекает M1K1 в N1. Точки отрезка NK не имеют общих точек с плоскостью DEF. В тех случаях, когда общих для заданных пересекающихся плоскостей точек нет (рис. 40), их нужно каким-либо образом построить. Например, чтобы найти общие точки для заданных плоскостей общего положения Р и Q, рассечём эти плоскости вспомогательными плоскостями S и T . Плоскость S с заданными плоскостями пересекается по прямым 1-2 и 3-4, которые между собой пересекутся в точке М. Аналогично плоскость Т с заданными плоскостями пересекается по прямым 5-6 и 7-8, которые между собой пересекутся в точке N. Отрезок прямой МN – линия пересечения плоскостей Р и Q. 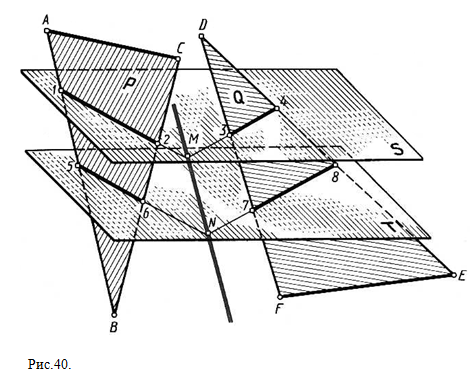
Решение этой задачи в ортогональных проекциях показано на рис.41. 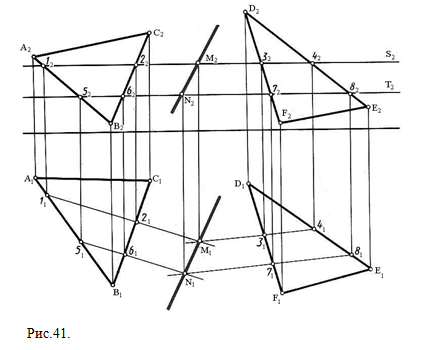
Пересекающиеся плоскости в частном случае могут быть перпендикулярными. Для выявления случаев перпендикулярности надо помнить, что если две плоскости взаимно перпендикулярны, то одна из них проходит через перпендикуляр к другой плоскости. На рис. 37 дан комплексный чертеж взаимно перпендикулярных пересекающихся плоскостей: одна фронтально проецирующая Σ ( Σ2), а вторая - общего положения (ABC) -содержит в себе перпендикуляр АВ к плоскости Σ(AB||П2; A2B2_|_Σ2). Две плоскости в общем случае могут пересекаться в бесконечности. Тогда имеет место параллельность этих плоскостей. Одна плоскость параллельна другой, если две пересекающиеся прямые, принадлежащие одной плоскости, будут соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости. На рис. 36 Р и Q параллельны, так как пересекающиеся прямые а и b, принадлежащие плоскости Р соответственно параллельны прямым с и d, расположенным в плоскости Q (а || с, b || d). Из курса геометрии известно, что две параллельные плоскости пересекаются с третьей, не параллельной им плоскостью, по параллельным прямым. Отсюда следует, что две параллельные плоскости Р и Q пересекутся с горизонтальной плоскостью проекций П1 по параллельным прямым Р1 и Q1. По параллельным прямым P2 и Q2 пересекутся они и с фронтальной плоскостью проекций П2, т. е. одноименные следы параллельных плоскостей будут параллельны. И, наоборот, если одноименные следы плоскостей на эпюре параллельны, то такие плоскости параллельны. Плоскости общего положения будут параллельны, если два любых одноименных следа параллельны между собой. Например, параллельными будут плоскости Р и Q, изображенные на рис. 42, у них параллельны горизонтальные следы Р1 и Q1, а также фронтальные следы P2 и Q2. 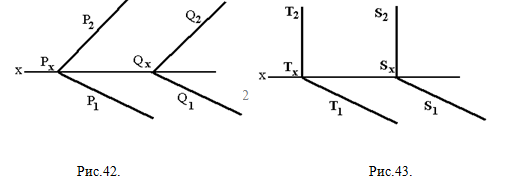
Проецирующие плоскости будут параллельны, если соответственно параллельны одноименные следы при общих точках схода. Например, параллельными будут горизонтально проецирующие плоскости Т и S, изображенные на рис. 43. Решение задач на параллельные плоскости сводится обычно или к построению плоскости, параллельной заданной, или к проверке параллельности двух заданных плоскостей. На рис. 44,а задана плоскость треугольника ABC и точка К, не при-надлежащая плоскости этого треугольника. Требуется через точку К провести плоскость, параллельную плоскости заданного треугольника ABC. Искомая плоскость может быть определена двумя пересекающимися прямыми, проведенными через точку К и параллельными двум пересекающимся прямым, принадлежащим заданной плоскости треугольника. На рис. 44,б для этого через заданную точку К проведены прямая m, параллельная АВ, и прямая n, параллельная АС, у этих прямых будут параллельны одноименные проекции (m1 \\ A1B1 и m2 || A2B2, а n1|| A1C1 и n2|| A2C2). 
Чтобы проверить параллельность двух заданных плоскостей, нужно в одной из них провести две какие-либо пересекающиеся прямые и попытаться построить в другой плоскости прямые, параллельные проведенным в первой плоскости. Если эта задача выполнима, то плоскости параллельны. Если же во второй плоскости не удастся провести прямые, параллельные проведенным в первой, то заданные плоскости не параллельны. |
