

|
Взаимное расположение двух плоскостей Две плоскости в пространстве могут быть параллельными или пересекаться. Параллельными будут плоскости, если одна из них задана пересекающимися прямыми, параллельными пересекающимся прямым, задающим вторую плоскость; на рис. 36 показаны параллельные плоскости, причем а || с, a b || d. Если плоскости пересекаются, то линия их пересечения — прямая. Плоскости, перпендикулярные между собой, представляют случай их пересечения, когда угол между плоскостями составляет 90°. ЗАПОМНИТЕ! Плоскости в пространстве могут пересекаться или быть параллельными, при этом: 1. Линия пересечения двух плоскостей определяется либо двумя точками, одновременно принадлежащими заданным плоскостям, либо одной общей точкой и известным направлением этой прямой линии. 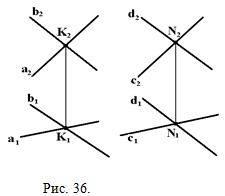
2. Если одна из пересекающихся плоскостей горизонтальная или фронтальная плоскость уровня, то линия пересечения плоскостей будет, соответственно, горизонталью или фронталью. 3. Точки, принадлежащие линии пересечения двух плоскостей, определяются методом вспомогательных секущих плоскостей. При этом заданные плоскости пересекаются вспомогательной (чаще всего проецирующей или плоскостью уровня) и определяется точка, общая для всех трех плоскостей; эта точка и принадлежит искомой линии пересечения заданных плоскостей, повторив аналогичное построение, определяют вторую общую точку. 4. Признаком параллельности двух плоскостей является параллельность двух пересекающихся прямых одной плоскости, соответственно, двум пересекающимся прямым второй плоскости. Признаком параллельности плоскостей частного положения является взаимная параллельность их одноименных следов- проекций. |
