|
Изометрия плоских фигур, которые принадлежит плоскостям проекций или плоскостям уровня Построение изометрии многоугольников. ЗАПОМНИТЕ! Для построения изометрии плоского многоугольника необходимо построить изометрические проекции его вершин и соединить их между собой. Задача 1. Задан эпюр правильного треугольника АВС, П1 (рис.53,а). Построить изометрию треугольника АВС (Рис.54). ВНИМАНИЕ! При построении изометрии симметричных плоских фигур оси координат переносят в новое положение так, чтобы они совпали с осями симметрии фигуры, а точка их пересечения O' с её центром (Рис.53,б). 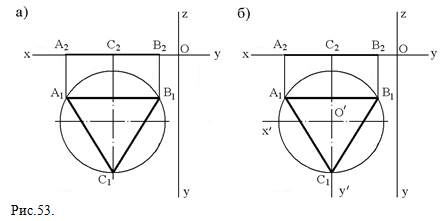 Рис.53.
Рис.53.
1) через произвольную точку O0 проводим аксонометрические оси X0 и Y0 (ось Z0 для построений не нужна); 2) на эпюре отметим точку 11 и измерим расстояния O'11 и O'С1, откладываем их по изометрической оси Х0, отметим точки 10 и С0; 3) через точку 10 параллельно оси X0 проведем линию; на эпюре измерим расстояние |A1l1|=|l1B1| и отложим его от точки 10 по этой прямой, отметим точки А0 и В0; 4) соединим точки А0,В0,С0 и получим изометрию правильного треугольника АВС, который принадлежит плоскости П1. 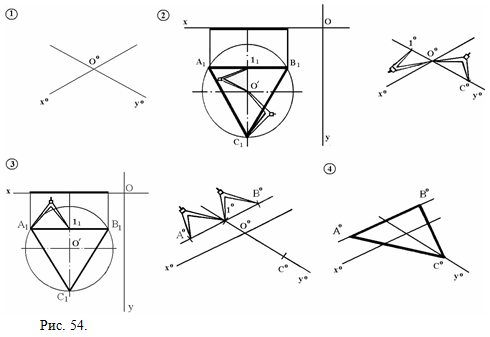 Рис. 54.
Рис. 54.
Задача 2. Задан эпюр правильного пятиугольника АВСDE, ABCDE ∈П2. Построить изометрию пятиугольника АВСDE (Рис.55). 1) через произвольную точку О0 проводим аксонометрические оси Х0 и Z0 (ось Y0 для построений не нужна); 2) на эпюре отметим точки 12 и 22; измерим расстояния 12, 22 и А2, отложим их по изометрической оси Х0, отметим 10,20,А0; 3) через точки 10 и 20 параллельно оси Z0 проведем линии; на эпюре измерим расстояния |l2B2|=|l2E2| и |C222|=|22D2| и отложим их на этих линиях, отметим точки В0, Е0 и С0, D0. 4) Соединим А0,В0,С0,D0,Е0 и получим изометрию правильного пятиугольника АВСDE, который принадлежит плоскости П2. 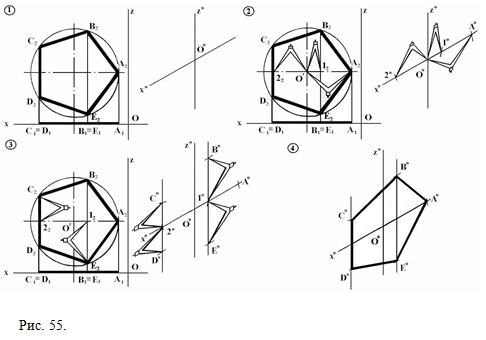 Рис. 55.
Рис. 55.
Задача 3. Задан эпюр правильного шестиугольника АВСDEF, который принадлежит профильной проекции. Построить изометрию шестиугольника (Рис.56). 1) через произвольную точку О0 проводим изометрические оси и Y0 (ось Х0 для построений не нужна); 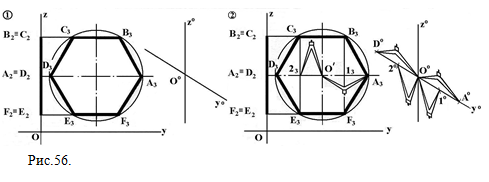 Рис.56.
Рис.56.
2) на эпюре отметим точки 13 и 23, измерим расстояния O'13= O'23 и O'D3 =O'A3 , отложим их по оси Y0 , отметим точки 10,20 и А0, D0 ; 3) через точки 10 и 20 проведем линии параллельно оси Z0 ; на эпюре измерим расстояние |l3B3|=|l2F3| =|C323|=|23E3| и отложим его на этих линиях, отметим точки В0,С0,Е0,F0. 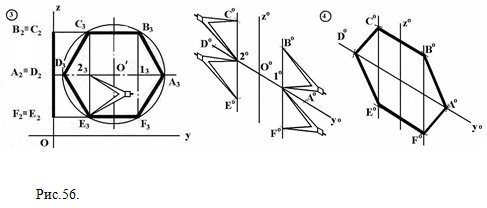 Рис.56.
Рис.56.
4) Соединим точки А0 В0 С0 D0 E0 F0 и получим изометрию правильного шестиугольника, принадлежащего плоскости П3. ЗАПОМНИТЕ! Для построения изометрических проекций вершин несимметричных многоугольников необходимо строить координатную ломаную каждой вершины в системе изометрических осей (рис.57). 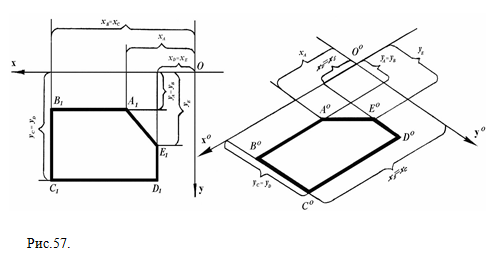 Рис.57.
Рис.57.
11.2. Построение изометрии окружности Окружности в аксонометрических проекциях проецируются в виде эллипсов. Длина большой оси эллипса в прямоугольной изометрии равна 1,22 D, длина малой оси 0,71 D, (D – диаметр окружности). Для упрощения построения стандарт рекомендует эллипс заменять на овал, большая и малая оси которого приблизительно соответственно равны большой и малой оси эллипса. Задача 1. построить изометрию окружности диаметром D, которая принадлежит плоскости П1 (рис.58, 59). I способ 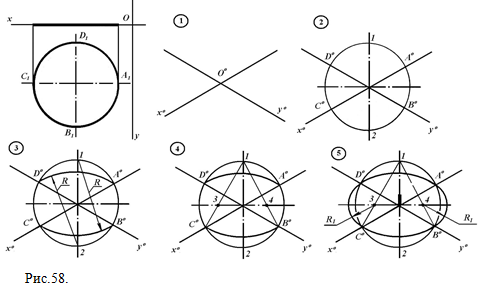 Рис.58.
Рис.58.
1) через произвольную точку О0 проводим изометрические оси Х0 и Y0 (рис.58); 2) с центром в точке О0 проводим окружность, диаметр которой равен диаметру заданной окружности, отметим точки А0,В0,С0,D0, а также точки 1 и 2 – точки пересечения окружности с ее вертикальным диаметром; 3) с центром в точках 1 и 2 проводим дуги радиуса R=|2A0|=|2D0=|1B0|=|1C0| , из точки 1 проводим дугу С0В0, из точки 2 – дугу А0D0. 4) Соединим точку 1 с точками С0 и В0, отметим точки 3 и 4 – точки пересечения проведенных прямых с горизонтальным диаметром окружности; 5) С центром в точке 3 проводим дугу А0D0, с центром в точке 4 – дугу А0В0, при этом радиус дуг R1 =|3C0|=|3D0|=|4B0|=|4A0|. ЗАПОМНИТЕ! Большая ось овала всегда перпендикулярна той аксонометрической оси, которая отсутствует в плоскости заданной окружности.II способ 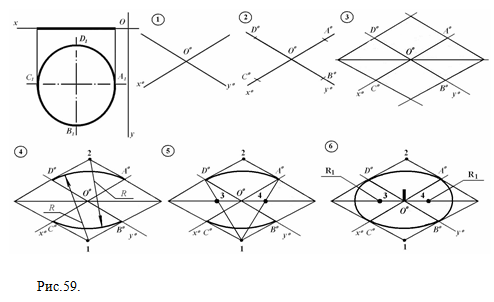 Рис.59.
Рис.59.
1) с центром в произвольной точке О0 проводим изометрические оси Х0 и Y0 (рис.59); 2) от точки О0 по осям откладываем расстояния, равные радиусу окружности, отметим точки А0,В0,С0,D0; 3) через точки А0 и С0 проводим прямые, параллельные оси Х0, через точки В0 и D0 – прямые, параллельные оси Y0; получаем ромб со сторонами, равными диаметру окружности; ВНИМАНИЕ! На большой диагонали ромба располагается большая ось овала. 4) из вершин тупых углов (точки 1 и 2) проводим дуги А0В0 и С0 D0радиусом R=|2B0|=|2C0|=|1A0|=|1D0| ; 5) соединим точку 1 с точками А0 и D0, отметим точки 3 и 4 – точки пересечения проведенных прямых и большой диагонали; 6) с центром в точке 3 проводим дугу C0 D0, с центром в точке 4 – дугу В0A0, радиус дуг R1; =|3C0|=|3D0|=|4B0|=4A0|;На рис. 60,а показано построение изометрии окружности, которая принадлежит фронтальной плоскости проекций, на рис.60,б – построение окружности, принадлежащей плоскости П3. 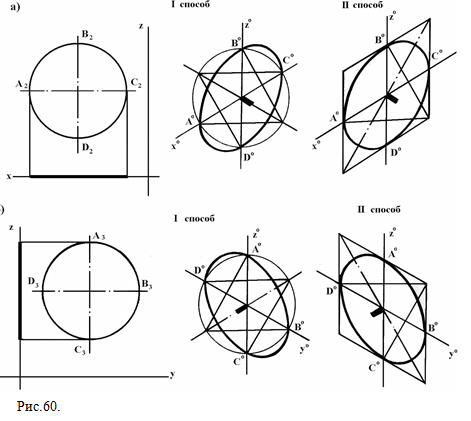 Рис.60.
Рис.60.
Структурно- логическая схема § 11 дана на стр. 46. Схема стр.46 ИзометрияПЛФ ЗАДАНИЯ 1. Ответьте на вопросы.
2. Выполните в тетради упражнения. 1. Постройте эпюр и изометрию плоскости АВС и прямой с, которая принадлежит плоскости АВС. 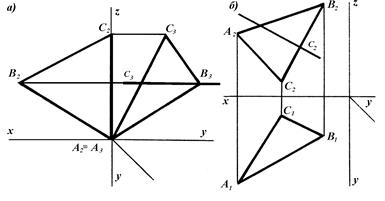
2. Постройте эпюр и изометрию плоскости АВС и точки Е, . 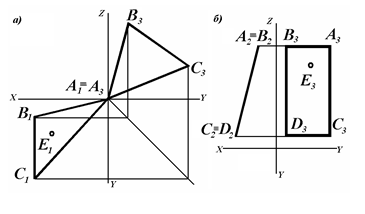
3. По эпюру плоскости АВС и прямых b, c, d определите какие прямые принадлежат плоскости. 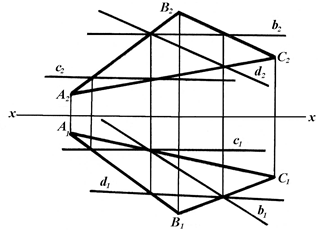
4. Достройте фронтальную проекцию треугольника АВС, если известно, что точка F принадлежит плоскости этого треугольника. 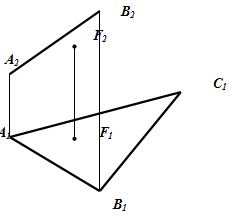
5. Постройте в плоскости треугольника АВС прямые уровня. 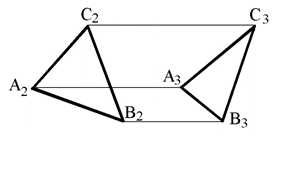
6. Построить недостающие проекции прямых m и n, лежащих в плоскости треугольника АВС. 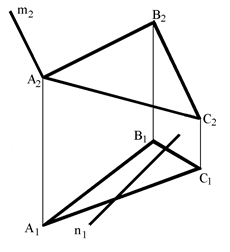
7.Определите точку пересечения прямой с плоскостью и видимость прямой относительно плоскости. 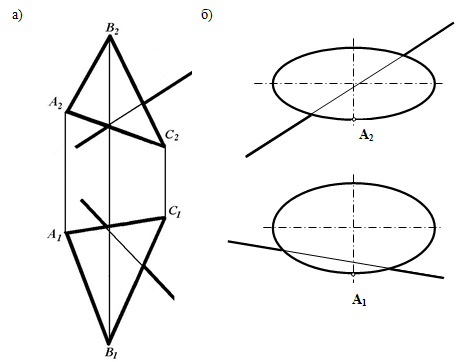
8. Постройте горизонтальную и фронтальную проекции линии пересечения плоскостей и определите относительную видимость треугольников АВС и DEF. Координаты точек: А (20;80;40), В (40; 30; 75), С (80; 45; 45), D (15; 50; 80), E (70; 90; 90), F (35; 15; 10). 9. Постройте изометрию правильного шестиугольника АВСDEF, вписанного в окружность, диаметр которой 50 мм, АВСDEF ¦ П3. 10. Постройте изометрические проекции плоских фигур:
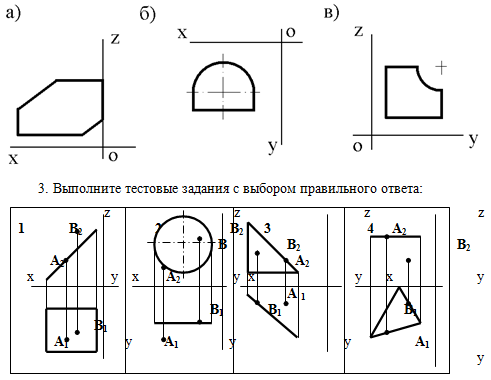
1. Горизонтально проецирующая плоскость задана на рисунке … А. 1. Б. 2. В. 3. Г. 4. Д. Такого рисунка нет. 2. Фронтально проецирующая плоскость задана на рисунке … А. 1. Б. 2. В. 3. Г. 4. Д. Такого рисунка нет. 3. Точка В расположена над плоскостью на рисунке … А. 1. Б. 2. В. 3. Г. 4. Д. Такого рисунка нет. 4.Точка А принадлежит фронтально проецирующей плоскости на рисунке … А. 1. Б. 2. В. 3. Г. 4. Д. Такого рисунка нет. 5. Плоскость проецируется на горизонтальную плоскость проекций в натуральную величину на рисунке … А. 1. Б. 2. В. 3. Г. 4. Д. Такого рисунка нет. 6. Плоская фигура расположена параллельно фронтальной плоскости проекций на рисунке … А. 1. Б. 2. В. 3. Г. 4. Д. Такого рисунка нет. 7. Плоскость расположена параллельно горизонтальной плоскости проекций на рисунке … А. 1. Б. 2. В. 3. Г. 4. Д. Такого рисунка нет. 8. Точка В принадлежит плоскости уровня на рисунке … А. 1. Б. 2. В. 3. Г. 4. Д. Такого рисунка нет. |