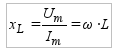|
Лекция №2
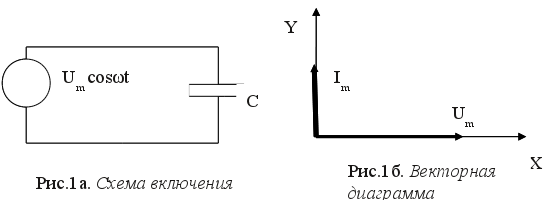
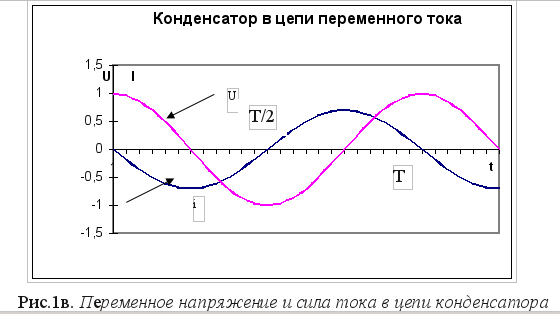
Разность фаз между силой тока в конденсаторе и напряжением на нём. Предположим, что в качестве нагрузки генератора переменного тока используется конденсатор электроемкостью С (рис. 1а). Переменное напряжение на обкладках конденсатора изменяется по закону: u = Umcosωt. В результате периодически повторяющихся процессов зарядки и разрядки конденсатора в цепи возникает переменный ток (ток проводимости в подводящих проводах и равный ему ток смещения между обкладками конденсатора). Установим связь между амплитудами переменного напряжения и тока в цепи. Электрический ток в цепи возникает в результате изменения заряда конденсатора:i=dq / dt Заряд на его обкладках изменяется по закону: q = Сu = CUmcosωt. Следовательно, сила тока i=dq / dt=-Im sinωt.
График зависимости силы тока от времени представлен на рис.1в. Для изображения силы тока на векторной диаграмме удобно представить выражение для силы тока в виде: I=Im cos(ωt +π/2). Начальная фаза колебаний напряжения равна нулю, а тока равна π/2 (рис.1б). Колебания силы тока в цепи конденсатора опережают по фазе колебания напряжения на его обкладках на π/2.
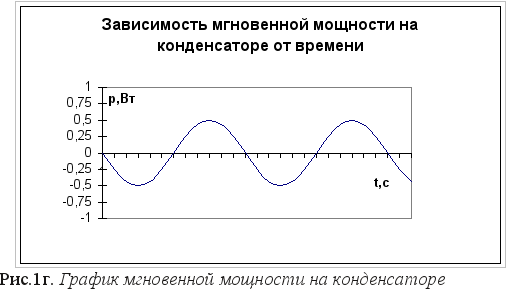
Мгновенная мощность переменного тока на конденсаторе определяется выражением p = iu = -0,5 Im Umsin2ωt.
Из графика зависимости мгновенной мощности на конденсаторе от времени (рис.1г) следует, что среднее значение мощности переменного тока на конденсаторе за период Т равно нулю. Принято говорить, что элементы цепи, для которых средняя мощность переменного тока равна нулю, обладают реактивным сопротивлением. Для этих элементов разность фаз колебаний силы тока и напряжения составляет π/2. Емкостное сопротивление Реактивное сопротивление конденсатора называется емкостным сопротивлением. Емкостное сопротивление (или сопротивление конденсатора по переменному току) определяется по закону Ома: 
Катушка индуктивности в цепи переменного тока Разность фаз между силой тока в катушке и напряжением на ней. Предположим, что в качестве нагрузки генератора переменного тока включена катушка индуктивностью L (рис. 1.а).
Для изображения силы тока на векторной диаграмме удобно представить выражение для силы тока в виде: i = Im сos(ωt – π/2) Начальная фаза колебаний напряжения равна нулю, а начальная фаза колебаний тока Графиком зависимости силы тока от времени является синусоида (рис. 2 в) Колебания силы тока в катушке индуктивности отстают по фазе на π/2 от колебаний напряжения на ней.
Индуктивное сопротивление Переменное напряжение, созданное генератором на концах катушки, изменяется по закону: и = Umcosωt Найдем закон изменения силы тока в катушке. При изменении силы тока в катушке возникает ЭДС самоиндукции: Еsi= - Ldi / dt В любой момент времени ЭДС самоиндукции равна по модулю противоположна по знаку напряжению на концах катушки, созданному внешним генератором можно записать в виде уравнения: Ldi / dt= Umcosωt Будем искать решение этого уравнения в виде: i = Imsinωt Подстановка решения в уравнение дает: ωLImcosωt = Umcosωt Следовательно, амплитуда силы тока Im в катушке связана с амплитудой переменного напряжения Um законом Ома:
где xL = ωL — индуктивное сопротивление катушки. Индуктивное сопротивление прямо пропорционально частоте переменного тока. При увеличении частоты тока вихревое электрическое поле заметно препятствует тем изменениям тока, которые его вызвали. Мгновенная мощность переменного тока в катушке определяется выражением p = iu = 0,5ImUmsin2ωt.
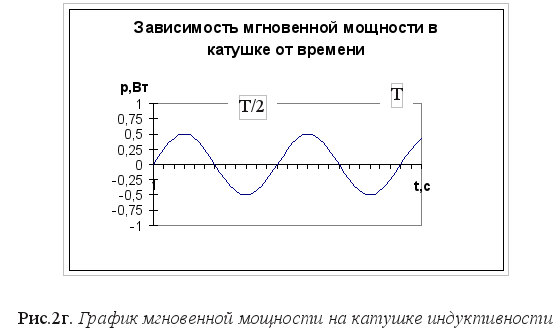
Из графика зависимости мгновенной мощности в катушке от времени (рис.2г) следует, что среднее значение мощности переменного тока в катушке индуктивности за период Т равно нулю. Индуктивное сопротивление является реактивным сопротивлением. Вопросы и задачи к лекции №2 Вопросы 1. Почему постоянный ток не может протекать через конденсатор?
Задачи
Приложение Векторные диаграммы для описания переменных токов и напряжений Представление гармонического колебания на векторной диаграмме. Переменное напряжение в сети изменяется с течение времени по гармоническому закону.
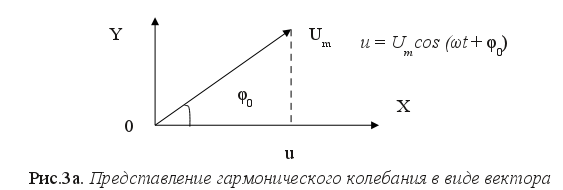
u = Umcos(ωt+ φ0), где Um — амплитуда (максимальное значение) напряжения, ω — круговая частота колебаний. Аргумент косинуса φ = ωt+ φ0 определяет фазу колебаний в момент времени t. Фаза колебаний — аргумент функции, описывающей гармонические колебания. При заданной амплитуде фаза определяет мгновенное значение колеблющейся величины. Начальная фаза колебаний φ0 — фаза колебаний в начальный момент времени, т. е. при t = 0. Для наглядного описания гармонических колебаний используется метод векторных диаграмм. В методе векторных диаграмм гармоническое колебание представляют в виде вектора. Модуль этого вектора равен амплитуде колебаний, а угол, образуемый вектором с осью X, равен начальной фазе колебаний (рис. 3а). Возможность такого представления гармонического колебания следует из взаимосвязи гармонического колебательного движения с вращением по окружности. Рассмотрим подробнее эту взаимосвязь, чтобы обосновать метод векторных диаграмм. Предположим, что вектор с модулем Im в начальный момент (t = 0) направлен по оси X. Если определить начальную фазу φ0 как угол, образуемый вектором с осью X в начальный момент времени, то φ0= 0. Пусть этот вектор вращается в плоскости XY с угловой скоростью &969 против часовой стрелки (рис. 3, б). Через время t вектор поворачивается на угол ωt.
ВОПРОСЫ
|

 />
/>