Построение разверток тел вращения

Поверхности геометрических тел вращения подразделяются на развертывающиеся, которые можно, разрезав по образующей, совместить с плоскостью без разрезов и складок, и неразвертывающиеся. К развертывающимся относятся, например, поверхности цилиндра и конуса. Примерами неразвертывающихся поверхностей могут служить поверхности шара и тора. Развертки этих поверхностей строят приближенно.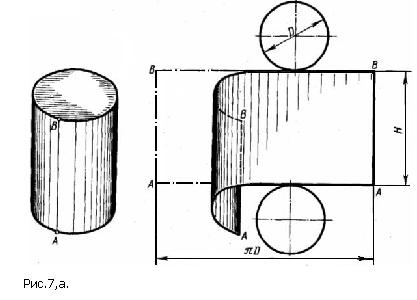

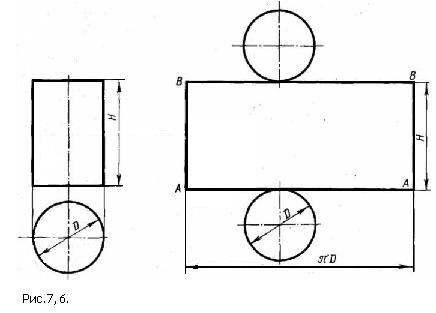
Рассмотрим построение развертки прямого кругового цилиндра (рис.7,а). Развертка его боковой поверхности – прямоугольник, одна сторона которого равна длине окружности основания πD, а другая – высоте цилиндра Н. Пусть диаметр основания цилиндра(D) равен 100 мм. Тогда длина развёртки боковой поверхности цилиндра равна 3,14*100=314 мм. Если высота цилиндра равна 200 мм, тогда мы чертим прямоугольник, длина которого 314 мм, а высота Н=200 мм. Чтобы получить полную развертку цилиндра к развёртке боковой поверхности пристроим два круга диаметром 100 мм – основания цилиндра (рис. 7,б).

Построение развертки прямого кругового конуса (рис. 8) заключается в построении боковой поверхности, которая развёртывается в круговой сектор, и круга - основания. Радиус сектора равен длине образующей конуса L . Угол при вершине сектора определяется по формуле:

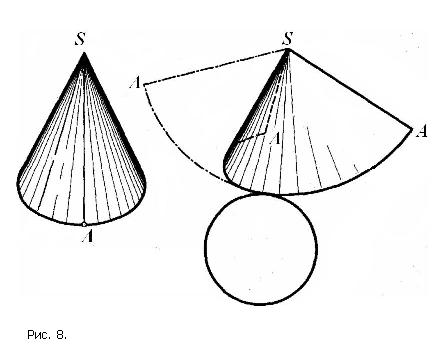
Рассмотрим построение развёртки прямого кругового конуса (рис.9). Она состоит из двух частей: кругового сектора (развёртки боковой поверхности конуса) и круга (основания).

Чтобы построить круговой сектор, надо знать радиус сектора и угол при вершине сектора или длину дуги сектора. Радиус сектора равен длине образующей конуса SA, например 200 мм. Зная диаметр основания, например 100 мм, рассчитаем угол при вершине: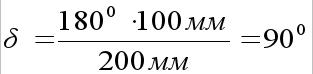

По этим данным построим развёртку поверхности прямого кругового конуса. Из произвольной точки S, как из центра, начертим дугу окружности, радиус которой равен натуральной величине образующей конуса SA (200 мм). На этой дуге отметим произвольную точку А и соединим её с вершиной – точкой S. Откладываем угол при вершине, равный 90°, проводим прямую до пересечения с дугой, получаем точку А₁. Мы построили развёртку боковой поверхности конуса.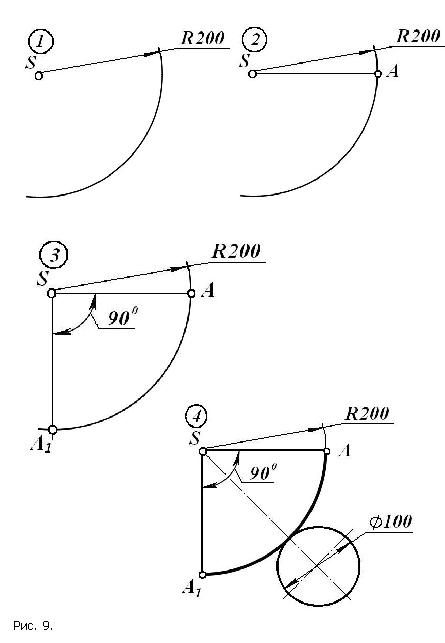

Затем к боковой поверхности конуса пристроим круг, диаметр которого равен 100 мм, - основание конуса. Мы построили развёртку полной поверхности прямого кругового конуса.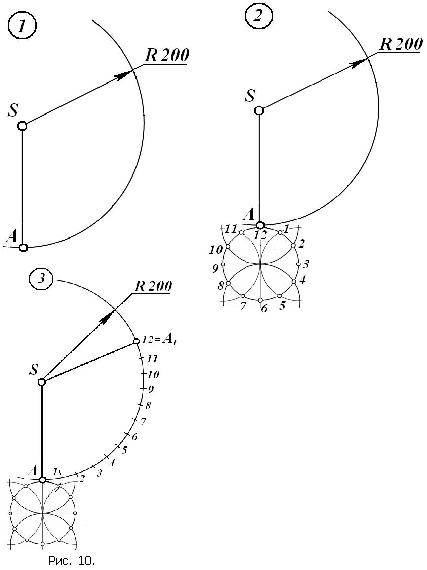

Развёртку прямого кругового конуса можно построить другим способом (рис.10). Из произвольной точки S, как из центра, начертим дугу окружности, радиус которой равен натуральной величине образующей конуса SA=200 мм. На этой дуге отметим произвольную точку А и соединим её с вершиной – точкой S. К точке А пристроим основание конуса – круг, диаметр которого равен 100 мм. И разделим его на 12 равных частей. От точки А отложим эти 12 отрезков по дуге сектора. Точку 12, которая совпадает с точкой А₁, соединим с вершиной - точкой S. Развертка поверхности конуса построена.

Чтобы не развёртке построить какую-либо точку, принадлежащую развёртываемой поверхности тела, необходимо предварительно через данную точку по поверхности провести линию. Затем эту линию нанести на развёртку и не ней отметить заданную точку (рис.1,4).

Рассмотренные задачи имеют важное значение, так как в техническом черчении часто необходимо строить развёртки с нанесением на них различных кривых линий, которые строят по отдельным точкам.