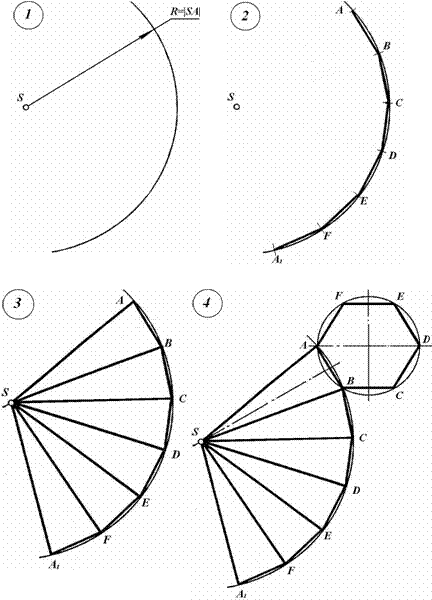
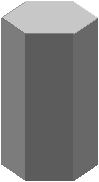1. Построение разверток многогранников
Разверткой поверхности тела называется плоская фигура, которая получается в результате совмещения всей поверхности тела с плоскостью. Такая плоская фигура получается, если поверхность тела разрезать по некоторой линии и совместить с плоскостью.

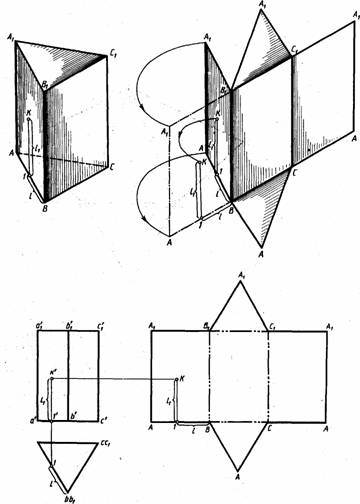
рис.1

Развертка многогранников получается последовательным совмещением с плоскостью его граней. На рис. 1 изображена прямая треугольная призма АВСА₁В₁С₁. Разрежем поверхность призмы по ребрам АА₁, АВ, АС, А1В₁  и А₁С₁ и совместим основания призмы и боковые грани АВ В₁А₁ и САА₁С₁ с плоскостью грани ВСС₁ В₁. Полученная фигура  А₁В₁А₁С₁А₁АСАВА будет разверткой данной призмы.

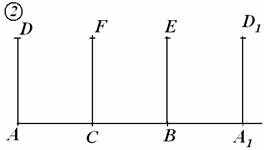
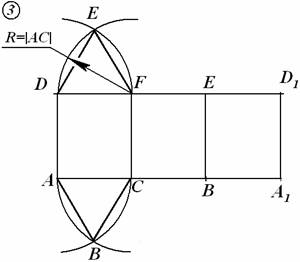
рис. 2

Рассмотрим   подробно   построение   развёртки   правильной треугольной призмы АBCDEF(рис.2). Чтобы построить развертку тела необходимо знать натуральные величины всех частей его поверхности. Все боковые грани призмы – прямоугольники (ABED, ADFC, DCFE),  которые равны друг другу, так как призма правильная. Развертка боковой поверхности данной призмы представляет собой три таких прямоугольника. Длина развёртки боковой поверхности равна сумме сторон треугольника ABC, который находится в основании, а высота равна высоте призмы (длине рёбер AD, BE,CF).
Для построения развёртки на горизонтальной  прямой линии (рис.2) отложим три равных отрезка АС=СВ=ВА₁. Из точек А, С, В и А₁ проведём перпендикуляры, равные высоте призмы, и отметим точки D, F, E, D₁. Соединив эти точки прямой линией, получим прямоугольник ADA₁D₁ – это развёртка боковой поверхности призмы. К развёртке боковой поверхности призмы c помощью циркуля достроим два основания – правильные треугольники АВС и DEF.

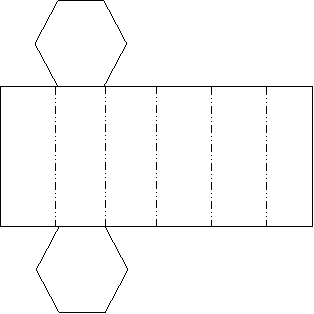
рис. 3

Аналогично выполняется построение правильной прямой шестиугольной призмы (рис.3).

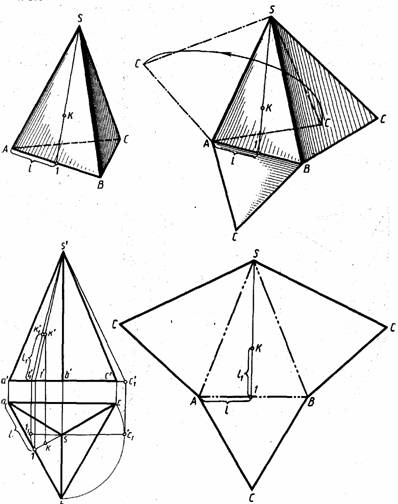
рис. 4

На рис. 4 показано построение раз­вертки правильной прямой треугольной пирамиды SАВС. Поверхность пирамиды разрезана по ребрам SС;  СА;  ВС. Осно­вание   и   боковые  грани SАС и SВС совмещены с гранью SАВ. Полученная плоская фигура SСАСВС будет разверткой треугольной пирамиды. Боковые грани пирамиды — треугольники — построены на развертке способом засечек.
Действительные размеры боковых ре­бер пирамиды определены способом вра­щения. Так, например, ребро SС повер­нуто вокруг оси, перпендикулярной плос­кости П₁ и проходящей через вершину S, до положения SС₁.В этом положении ребро будет параллельно плоскости П₂ и фронтальная проекция s'с'₁ равна дейст­вительным размерам ребра. Стороны основания пирамиды проецируются в дей­ствительную величину на плоскость П₁.
Изображенные на развертках ребра многогранников, по которым будет сги­баться развертка, чтобы получить исход­ное тело, называются линиями сгиба и выделяются на чертеже штрихпунктирной тонкой линией с двумя точками.

рис. 5

Рассмотрим подробно построение развёртки поверхности правильной прямой шестиугольной пирамиды SABCDEF(рис.5), основание которой параллельно профильной плоскости проекции и проецируется на неё в натуральную величину.
Развертка боковой поверхности пирамиды представляет собой шесть равнобедренных треугольников – граней пирамиды. Все треугольники равны между собой. Основания этих треугольников равны сторонам правильного шестиугольника BCDEF. Боковые стороны треугольников равны боковым рёбрам пирамиды (SA).

рис. 6

По этим данным построим развёртку поверхности пирамиды (рис.6). Из произвольной точки S, как из центра, начертим дугу окружности, радиус которой равен натуральной величине бокового ребра пирамиды SА. На этой дуге отметим произвольную точку А.  От точки А по дуге отложим шесть хорд, длина которых равна длине ребра основания АВ. Отметим точки  A, B, C, D, E, F, А₁. Соединим эти точки с точкой S. Мы построили развёртку боковой поверхности пирамиды. Затем к одному из оснований равнобедренных треугольников, например к АВ, пристроим правильный шестиугольник – основание пирамиды.