Графики функций, содержащих модуль

Рассмотрим построение графиков функций:

y=|f(x)|; y=f(|x|); y=|f(|x|)|

7.1) Построение графика функции y=|f(x)|

Пусть дана функция y=|f(x)|. Для построения графика функции y=|f(x)| рассмотрим: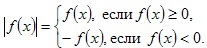

Отсюда следует, что график функции y=|f(x)| совпадает с графиком функции
y=f(x) там, где f(x)≥0 и симметричен графику функции y=f(x) относительно оси ОХ там, где f(x)<0.

Смотри рисунок:

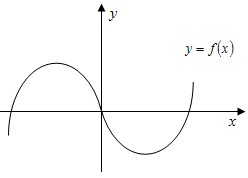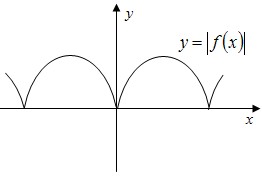
Пример №1: Построить график – схему функции y=|x²−5x+4|

1.0) Построим график функции y=x²−5x+4.

График функции у – парабола с ветвями, направленными вверх.

1.1) Найдем вершину параболы:

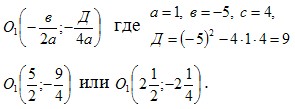
1.2) Найдем точки пересечения с осями координат:

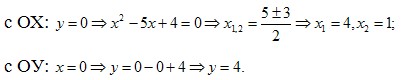
Имеем (4;0)(1;0)(0;4) - точки пересечения графика с осями координат

2.0) Построим график функции y=|y₁|. Для этого берем часть графика, где y<0, и поднимаем симметрично оси ОХ.

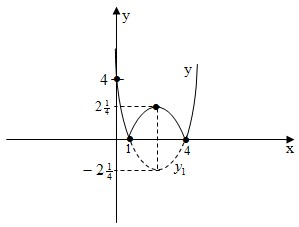
7.2) Построение графика функции y=f(|x|)

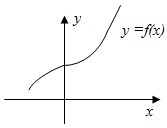
f(|x|)=f(x), если х≥0. Значит, график функции f(|x|)=f(x) совпадает с графиком y=f(x) там, где x≥0.

f(|x|) - четная функция, потому что f(x)=f(|x|) .

Значит, график функции y=f(|x|) симметричен относительно оси ОУ.

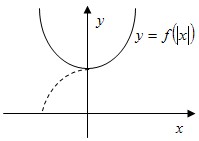
Пример №2. Построить график – схему функции y=x²−5|x|+4

1.0) Построим график функции y₁=x²−5x+4 (Используем пример №1)

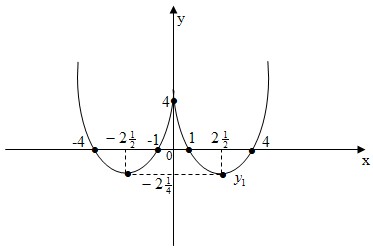
2.0) Построим график функции y=y₁(|x|)

Для этого строим во II и III квадратах часть параболы, симметричную относительно оси ОУ части параболы y₁, расположенной в I и II квадратах.

7.3) Построение графика функции y=|f(|x|)|

Для построения графика функции y=|f(|x|)| нужно построить график y=f(x), затем перейти к графику функции y=f(|x|), а от него к графику y=|f(|x|)|.

Пример №3. Построить график – схему функции y=|x²−5|x|+4|.

1.0) Построим график функции y=x²−5x+4 (Используем пример №1)

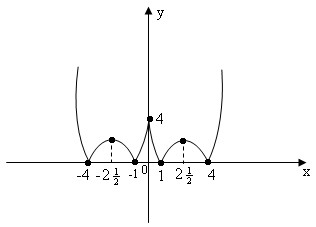
2.0) Построим график функции y=|y₁| (аналогично примеру №1)

3.0) Построим график функции y=|y₁(|x|)| (аналогично примеру №2)