|
6. Виды функций
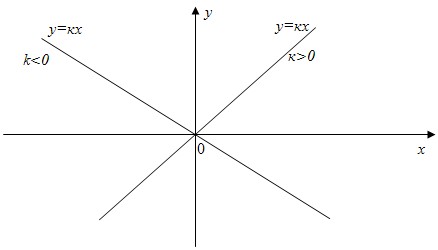
6.1)Функция y=kx
Функция y=kx, где k≠0, называется прямой пропорциональной зависимости, число к – коэффициент пропорциональности.
6.1.1) Свойства функции ;
- Д(f)=R, x∈R.
- E(f)=R, y∈R.
- y=0, при x=0, функция имеет только одну точку пересечения с осями координат (0;0).
- Функция нечетная, так как y(−x)=−y(x) ее график симметричен относительно начала координат.
- При k>0 - функция монотонно возрастает на всей области определения.
При k<0 - функция монотонно убывает на всей области определения.
- Функция не имеет экстремумов.
- Функция не ограничена.
- Функция не имеет периода.
- График функции – прямая линия.
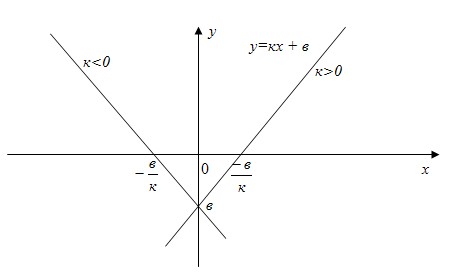
6.2) Функция y=kx+b
Функция вида y=kx+b, k≠0 , называется линейной, где к – угловой коэффициент.
6.2.1) Свойства функции y=kx+b
- Д(f)=R, x∈R.
- E(f)=R, y∈R.
- y=0, kx+b=0, x=−
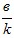 ; x=0; y=b. График пересекает оси координат в двух точках (− ; x=0; y=b. График пересекает оси координат в двух точках (−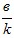 ;0)(0;b) ;0)(0;b)
- Функция общего вида: y(−x)≠y(x); y(−x)≠−y(x)
- При k>0 - функция монотонно возрастает на R.
При k<0 - функция монотонно убывает на R.
- Функция не имеет экстремумов.
- Функция не ограничена.
- Функция не имеет периода.
- График функции – прямая линия.
6.3) Функция y=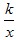
Функция вида y=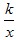 (k≠0) называется обратной пропорциональной зависимостью, где k - коэффициент обратной пропорциональности. (k≠0) называется обратной пропорциональной зависимостью, где k - коэффициент обратной пропорциональности.
6.3.1) Свойства функции y=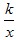
- Д(f)=(−∞;0)∪(0;+∞).
- E(f)=(−∞;0)∪(0;+∞).
- Функция не имеет нулей.
- Функция нечетная, ее график симметричен относительно начала координат.
- При k>0 функция монотонно убывает в каждом интервале из области определения, так как при x2>x1⇒f(x2)>f(x1).
При k<0 функция монотонно возрастает в каждом интервале области определения.
- Функция не имеет экстремумов.
- Функция не ограничена.
- Функция не имеет периода.
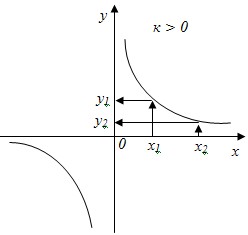
- График этой функции – гипербола.
График функции не пересекает осей координат, но ветви гиперболы неограниченно приближается к ним. Говорят, что оси ОХ и ОУ – асимптоты гиперболы.
 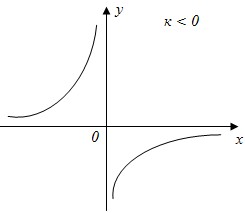
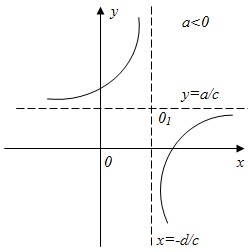
6.4) Функция y=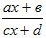
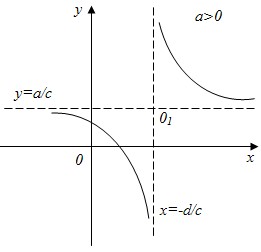
Функция вида y=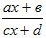 называется дробно-линейной функцией, где числитель и знаменатель – линейные функции (a≠0, b≠0, c≠0, d≠0) называется дробно-линейной функцией, где числитель и знаменатель – линейные функции (a≠0, b≠0, c≠0, d≠0)
Разделив числитель на знаменатель, получим y=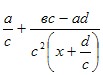 , x=− , x=−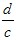 , y= , y=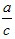 - асимптоты. - асимптоты.
6.4.1) Свойства функции y=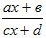
- Д(f)=(−∞;−
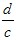 )∪(− )∪(−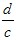 ;+∞). ;+∞).
- E(f)=(−∞;−
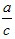 )∪(− )∪(−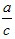 ;+∞). ;+∞).
- Функция общего вида.
- y=0; x=−
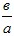 ; x=0; y= ; x=0; y=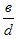 . График пересекает оси координат в двух точках (− . График пересекает оси координат в двух точках (−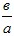 ;0) и (0; ;0) и (0;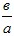 ). ).
- При a>0 график функции убывает.
При a<0 график функции возрастает.
- Максимума и минимума функция не имеет.
- Функция не ограничена.
- Функция периода не имеет.
- График функции гипербола.
6.5) Квадратичная функция
Функция вида y=ax2+bx+c называется квадратичной функцией, где a, b, c – const, a≠0, х – переменная.
Рассмотрим частные случаи квадратичной функции.
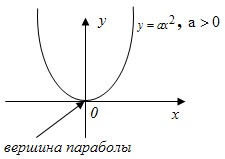
6.5.1) Функция y=ax2 (a≠0)
6.5.1.1) Свойства функции y=ax2 (a≠0)
- Д(f)=R.
- E(f)=[0;+∞).
- Функция имеет один нуль: y=0 при x=0 .
- Функция четная, ее график симметричен относительно оси ОУ.
- Если a>0, то при x∈(−∞;0) функция монотонно убывает; при x∈(0;+∞) функция монотонно возрастает.
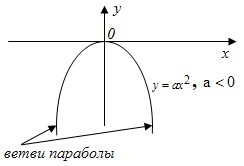
Если a<0, то при x∈(−∞;0) функция монотонно возрастает; при x∈(0;+∞) функция монотонно убывает.
- Функция имеет минимум ymin=0 при a>0; функция имеет максимум ymax=0 при a<0 в точке x=0.
- Функция y=ax2 ограничена снизу, ax2≥0, при a>0; ограничена сверху, ax2≤0, при a<0.
- Функция периода не имеет.
- График функции – парабола.
6.5.2) Функция y=ax2+bx+c, (a≠0)
Квадратичную функцию можно записать в виде: y=a(x-m)2+n.
Преобразуем квадратный трехчлен:
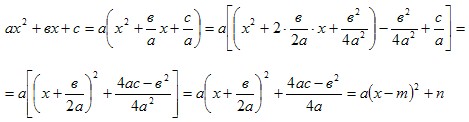 , ,
где 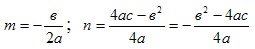
Получаем:
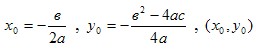 - вершина параболы. - вершина параболы.
6.5.2.1) Свойства функции y=ax2+bx+c, (a≠0)
- Д(f)=R.
- Если a>0, то E(f)=(−
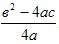 ;+∞). ;+∞).
Если a<0, то E(f)=(−∞;−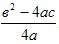 ). ).
- y=0; если b2-4ac<0, то функция нулей не имеет;
если b2-4ac=0, то функция имеет нуль при x=−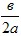 ; ;
если b2-4ac>0, то функция имеет два нуля:
x1=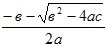 ; x2= ; x2=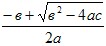 ; ;
- Если b≠0, то функция ни четная, ни нечетная;
при b=0 функция четная.
- При a>0 функция убывает на промежутке (−∞;−
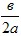 ) и возрастает на промежутке (− ) и возрастает на промежутке (−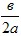 ;+∞). ;+∞).
При a<0 функция возрастает на промежутке (−∞;−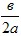 ) и убывает на промежутке (− ) и убывает на промежутке (−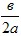 ;+∞). ;+∞).
- При a>0 функция имеет наименьшее значение при x=−
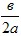 ; которое есть минимум функции, ymin= ; которое есть минимум функции, ymin=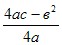 . Наибольшего значения нет. . Наибольшего значения нет.
При a<0 функция имеет наибольшее значение при x=−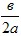 ; которое есть максимум функции, ymax= ; которое есть максимум функции, ymax=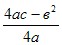 . Наименьшего значения функция не имеет. . Наименьшего значения функция не имеет.
- При a>0 функция ограничена снизу, y≥
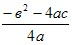 . .
При a<0 функция ограничена сверху, y≤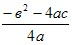 . .
- Функция периода не имеет.
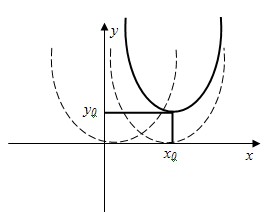
- График квадратичной функции y=ax2+bx+c есть парабола, а точка
(−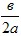 ; ;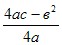 ) - вершина параболы. ) - вершина параболы.
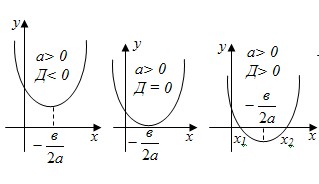 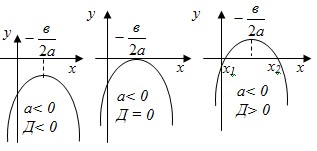
6.6) Построение графиков – схем некоторых функций
Иногда необходимо построить не точный график, а график – схему, это значит, нужно определить форму графика, найти экстремумы и точки пересечения с осями координат и координатной плоскости.
6.6.1) График – схема функции y=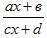 - гипербола - гипербола
1. Найдем вертикальную и горизонтальную асимптоты. Для этого определим область определения и область значения функции:
Д(y)=R{−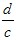 }⇒ x=− }⇒ x=−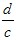 - вертикальная асимптота; - вертикальная асимптота;
E(y)=R{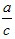 }⇒ x= }⇒ x=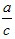 - горизонтальная асимптота. - горизонтальная асимптота.
(Найдем обратную функцию
cxy+dy=ax+b
cxy-ax=bdy
x(cy-a)=b-dy
x=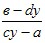
Из формулы видно, что y≠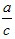 ). ).
2. Найдем точки пересечения графика функции с осями координат:
с ОХ: для этого решим уравнения: y=0 ⇒ 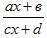 =0 ⇒ ax+b=0 ⇒ x=− =0 ⇒ ax+b=0 ⇒ x=−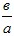
(−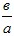 ;0) - точка пересечения с осью ОХ. ;0) - точка пересечения с осью ОХ.
с ОУ: для этого подставим в формулу функции значения х=0.
x=0 ⇒ y=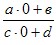 =0 ⇒ y= =0 ⇒ y=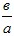
(0;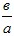 ) - точка пересечения с осью ОУ ) - точка пересечения с осью ОУ
По асимптотам x=−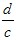 ; y= ; y=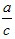 и точкам (0; и точкам (0;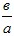 );(− );(−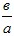 ;0) ;0)
Строим график – схему – гиперболу.
6.6.2) График – схема функции y=ax2+bx+c, (a≠0) парабола
1. Найдем форму параболы. Для этого определим знак коэффициента а.
Если a>0 ветви параболы направлены вверх.
Если a<0 ветви параболы направлены вниз.
2. Найдем координаты вершины параболы по формуле: O'(−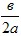 ;− ;−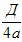 ) , где Д=b2-4ac. ) , где Д=b2-4ac.
3. Найдем точки пересечения графика функции с осями координат.
с ОХ: для этого решим квадратное уравнение.
y=0 ⇒ ax2+bx+c=0.
Имеем три варианта:
Если Д=b2-4ac>0 , график пересекает ось ОХ в двух точках
(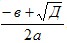 ;0);( ;0);(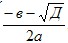 ;0). ;0).
Если Д=0, то график пересекает ось ОХ в одной точке (она вершина параболы) (−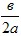 ;0). ;0).
Если Д<0, то график не пересекает ось ОХ (либо весь находится в I, II квадратах, либо – в III, IV).
с ОУ: для этого подставим в формулу функции значение x=0.
x=0 ⇒ y=a⋅0+b⋅0+c ⇒ y=c.
(о;с) – точка пересечения параболы с осью ОУ.
По форме, вершине и точкам пересечения с осями координат строим график – схему – параболу.
Например 2. Построить график – схему функции
График функции – парабола.
1. a=1>0 значит ветви параболы направлены вверх.
2. Найдем вершину параболы.
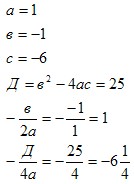
Тогда 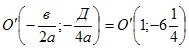
3. Найдем точки пересечения с осями координат:
с ОХ: y=0 ⇒ x2−x−6 ⇒ x1,2=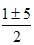 ⇒ x1=3 x2=2 . ⇒ x1=3 x2=2 .
Имеем (3;0) и (-2;0) – точки пересечения параболы с осью ОХ.
с ОУ: x=0 ⇒ y=−6.
Имеем (0;-6) – точка пересечения параболы с осью ОУ.
Построим схему параболы.
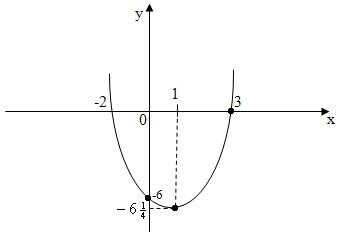
6.7) Функция y=ax
Функция вида y=ax, где a>0 и a≠0, называется показательной функцией.
6.7.1) Свойства функции y=ax
- Д(f)=R.
- E(f)=[0;+∞).
- x=0, y=1. Одна точка пересечения с осью ОУ:(0;1).
- Функция общего вида, так как a−x≠ax и a−x≠−ax.
- Если a>1, функция возрастает на всей области определения.
При 0<a<1 функция убывает на всей области определения.
- Экстремума нет.
- Функция не ограничена.
- Функция периода не имеет.
- График функции:
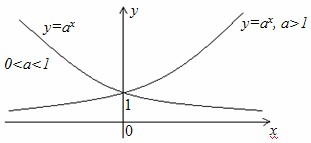
6.8) Функция y=logax
(читают: «Функция игрек равен логарифму числа х по основанию а).
Функция вида y=logax, где a>0, a≠0, - это функция, обратная к показательной функции y=ax.
6.8.1) Свойства функции y=logax
- Д(f)=(0;+∞).
- E(f)=R.
- y=0, x=1. Одна точка пересечения с осью ОХ(1;0).
- Функция общего вида.
- Если a>1, функция возрастает на промежутке (0;+∞).
При 0<a<1, функция убывает на промежутке (0;+∞).
- Экстремума нет.
- Функция не ограничена.
- Функция периода не имеет.
- График функции:
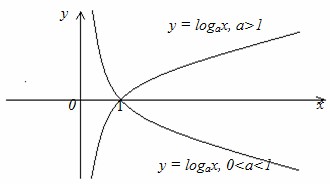
6.9) Тригонометрические функции
Функции вида y=sin x, y=cos x, y=tg x, y=ctg x - называются тригонометрическими функциями.
6.9.1) Свойства функции y=sin x;
- Д(f)=R.
- E(f)=[−1;1].
- y=0 при x=πk, k∈Z; x=0 при y=0. Точки (πk;0), где k∈Z, - нули функции.
- Функция y=sin x - нечетная, sin(−x)=−sin(x). График симметричен относительно начала координат.
- Функция y=sin x возрастает при x∈
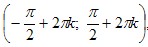 , k∈Z, и убывает при x∈ , k∈Z, и убывает при x∈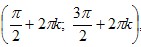 , k∈Z. , k∈Z.
- Функция y=sin x имеет минимальные значения, равные −1,
при x=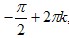 , k∈Z, и максимальные значения, равные 1, , k∈Z, и максимальные значения, равные 1,
при x=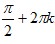 , k∈Z. , k∈Z.
(Ymax=1 при x=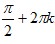 ; Ymin=−1 при x= ; Ymin=−1 при x=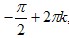 ). ).
- Функция ограничена: |sin x|≤1.
- Функция y=sin x - периодическая. Наименьший положительный период равен 2π, sin(x±2π)=sin x.
- График функции – синусоида.
-
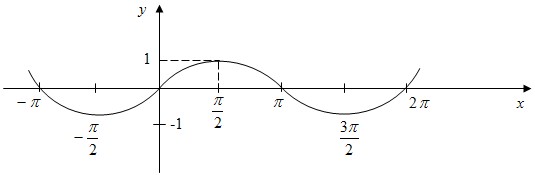
6.9.2) Свойства функции y=cos x;
- Д(f)=R.
- E(f)=[−1;1].
- y=0 при x=
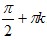 , k∈Z; x=0 при y=1. Точки ( , k∈Z; x=0 при y=1. Точки (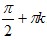 ;0), где k∈Z, - нули функции. ;0), где k∈Z, - нули функции.
- Функция y=cos x - четная: cos(−x)=cos(x). График симметричен относительно оси ОУ.
- Функция y=cos x возрастает при x∈(−π+2πk;2πk), k∈Z, и убывает при x∈(2πk;π+2πk), k∈Z.
- Функция y=cos x имеет минимальные значения, равные −1,
при x=π+2πk, k∈Z, и максимальные значения, равные 1,
при x=2πk, k∈Z.
(Ymax=1 при x=2πk; Ymin=−1 при x=π+2πk, k∈Z).
- Функция y=cos x ограничена: |cos x|≤1.
- Функция y=cos x - периодическая. Наименьший положительный период равен 2π, cos(x±2π)=cosx.
- График функции – косинусоида.
-
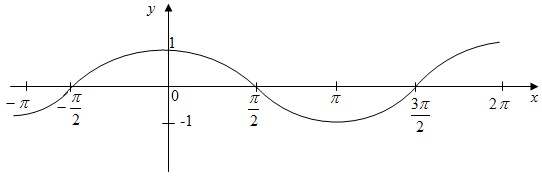
6.9.3) Свойства функции y=tg x
- Д(f)=R/{
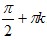 , k∈Z}. , k∈Z}.
- E(f)=R.
- y=0 при x=πk, k∈Z; x=0 при y=0. Точки (πk;0), где k∈Z, - нули функции.
- Функция y=tgx - нечетная: tg(−x)=−tg(x).
- Функция y=tgx возрастает в каждом из промежутков (−
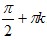 ; ;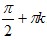 ) k∈Z. ) k∈Z.
- Экстремумов нет.
- Функция не ограничена.
- Функция y=tg x периодическая. Наименьший положительный период равен π, tg(x±π)=tg x.
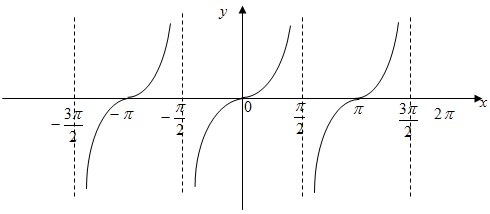
- График функции – тангенсоида.
-
6.10) Обратные тригонометрические функции
6.10.1) Свойства функции y=arcsin x
- Д(f)=[−1;1].
- E(f)=[−
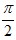 ; ;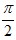 ]. ].
- arcsin x=0 при x=0.
- Функция y=arcsin x - нечетная: arcsin(−x)=−arcsin(x).
- Функция y=arcsin x возрастает на промежутке [−1;1].
- Функция y=arcsin x принимает свое наименьшее значение,
равное −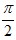 , при x=−1; наибольшее значение, равное , при x=−1; наибольшее значение, равное 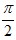 , при x=1. , при x=1.
- Функция y=arcsin x ограничена, −
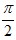 ≤arcsin x≤ ≤arcsin x≤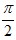 . .
- Функция y=arcsin x не имеет периода.
- График функции:
-
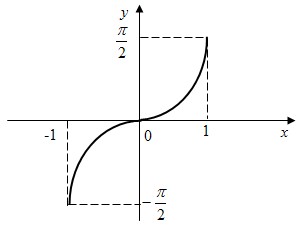
6.10.2) Свойства функции y=arccos x
- Д(f)=[−1;1].
- E(f)=[0;π].
- arccos x=0 при x=1; x=0 при y=
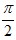 . .
- Функция y=arccos x - общего вида.
- Функция y=arccos x убывает на промежутке [−1;1].
- Функция y=arccos x принимает наибольшее значение,
равное π, при x=−1; наименьшее значение, равное 0, при x=1 .
- Функция y=arccos x ограничена, 0≤arccos x≤π.
- Функция y=arccos x не имеет периода.
- График функции:
-
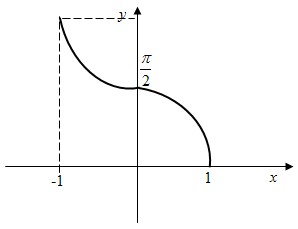
|
