|
4. Функция, обратная данной
Рассмотрим два соответствия 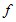 и и 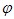 . .
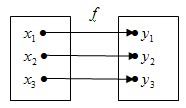 и и 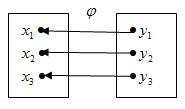
Соответствие 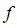 – функция, соответствие – функция, соответствие 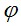 - тоже функция. Функция - тоже функция. Функция 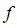 с областью определения Х и множеством значений У называется обратимой, если обратное ей соответствие между множеством У и Х является функцией. с областью определения Х и множеством значений У называется обратимой, если обратное ей соответствие между множеством У и Х является функцией.
В этом случае функцию 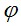 называют обратной функции называют обратной функции 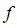 . .
Функция является обратимой тогда и только тогда, когда каждое свое значение она принимает только один раз, то есть функция монотонна.
Если y=f(x), то  если если 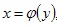 , то , то 
Если в выражении для обратной функции поменяем х на у, а у на х, потому что принято обозначать через х – аргумент, а буквой у – функцию, тогда y=f(x) - прямая функция, 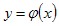 - обратная ей функция. - обратная ей функция.
Графики функций y=f(x) и 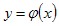 симметричны относительно прямой у = х. симметричны относительно прямой у = х.
Например. Получить обратную функцию для функции y=3x+2. Прямая функция y=3x+2 монотонно возрастает при 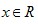 . Получим обратную ей функцию. Выразим х, получим . Получим обратную ей функцию. Выразим х, получим 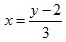 . Поменяем х на у, у на х. Тогда . Поменяем х на у, у на х. Тогда 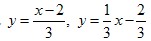 - обратная функция. Постоим их графики: - обратная функция. Постоим их графики:
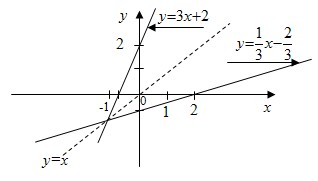
|
