|
3. Схема исследования функции
3.1) Область определения функции
Например:
а) 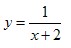
Выражение 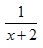 определено при всех действительных значениях х, кроме того значения, при котором знаменатель равен нулю, это значение х = -2. определено при всех действительных значениях х, кроме того значения, при котором знаменатель равен нулю, это значение х = -2.
Следовательно, 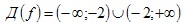 или Д(f)=R/{-2} или Д(f)=R/{-2}
б) 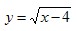
Выражение 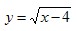 определено при тех х, для которых определено при тех х, для которых 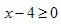 , то есть , то есть 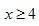 . Следовательно, . Следовательно, 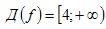 . .
3.2) Область значений функции
Например 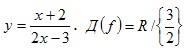
Область значений функции найдем, составив новую функцию, в которой аргумент (х) заданной функции рассматривается как функция, а функция (у) – как аргумент; то есть нужно в заданной функциональной зависимости выразить х через у.
Например: 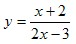
Находим функцию, обратную данной:
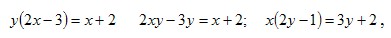 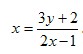
Выражение 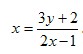 определено при всех действительных значениях у, кроме того значения, при котором знаменатель равен нулю, это значение определено при всех действительных значениях у, кроме того значения, при котором знаменатель равен нулю, это значение 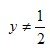 , то есть , то есть 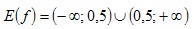
3.3) Точки пересечения графика функции с осями координат
Чтобы найти точку пересечения графика функции с осью ОУ, нужно вычислить y=f(0)
Например:
y=5x+1; y(0)=1. Точка (0;1) – точка пересечения графика с осью ОУ.
Чтобы найти точку пересечения графика функции с осью ОХ, нужно вычислить х, при котором f(x)=0.
Например:
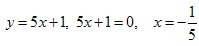 . Тогда . Тогда 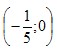 - точка пересечения с осью ОХ. Точки - точка пересечения с осью ОХ. Точки 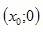 , в которых у = 0, называются нулями функции. , в которых у = 0, называются нулями функции.
3.4) Четность и нечетность функции.
Функция y=f(x) называется четной, если для любого х из области определения функции выполняется равенство: f(-x)=f(x)
Например: 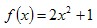
Имеем 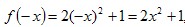 значит f(-x)=f(x) для всех х функция четная. значит f(-x)=f(x) для всех х функция четная.
График четной функции симметричен относительно оси ОУ.
Например
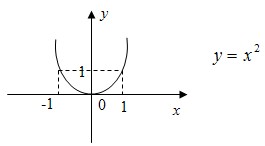
Функция y=f(x) называется нечетной, если для любого х из области определения функции выполняется равенство: f(-x)=-f(x).
Например: 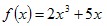
Имеем: 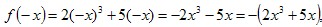 , значит f(-x)=-f(x) для всех х функция нечетная. , значит f(-x)=-f(x) для всех х функция нечетная.
График нечетной функции симметричен относительно начала координат. Например: 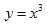
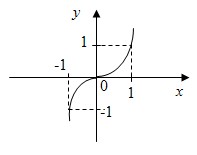
Если функция y=f(x) такая, что 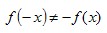 и и 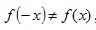 , то функция не является ни четной, ни нечетной. Такая функция называется функцией общего вида. , то функция не является ни четной, ни нечетной. Такая функция называется функцией общего вида.
3.5) Монотонность функции
Функция y=f(x) называется возрастающей на промежутке Х, если для любых x1 и x2 из Х таких, что x1<x2, выполняется неравенство f(x1)<f(x2) 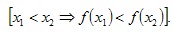 . .
Например: 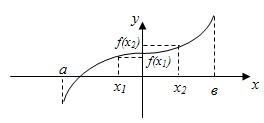
Функция у=f(x) называется убывающей на промежутке Х, если для любых x1 и x2 из Х, таких что x1<x2, выполняется неравенство f(x1)>f(x2) 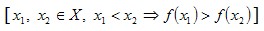 . .
3.6) Экстремумы функции
Пусть 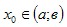 . Если для всех х из этого интервала, отличных от х0, выполняется неравенство f(x)<f(x0) , то при x=x0 функция имеет максимум (max) . Если для всех х из этого интервала, отличных от х0, выполняется неравенство f(x)<f(x0) , то при x=x0 функция имеет максимум (max)
Например: 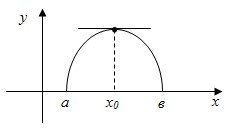
Если для всех х из этого интервала, отличных от х0, выполняется неравенство f(x)>f(x0) , то при x=x0 функция имеет минимумум (min)
Например: 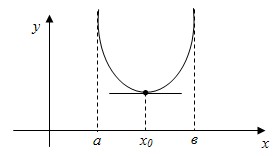
Монотонные функции не имеют экстремумов.
3.7) Ограниченность функции
Функция у=f(x) называется ограниченной на множестве Х, если существует такое число М, что для всех х из множества Х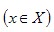 выполняется неравенство выполняется неравенство 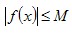 . .
Например: 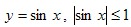 . .
Если для любого числа М найдется такое 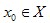 , что , что 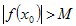 , то функция у=f(x) называется неограниченной на Х. , то функция у=f(x) называется неограниченной на Х.
Например: y=x3
3.8) Периодичность функции.
Функция у=f(x) называется периодической функцией с периодом Т, если выполняется равенство 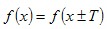 . .
Например: 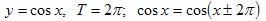
3.9) График функции.
Графиком функции у=f(x) называется множество точек координатной плоскости с координатами (х,f(x)), где 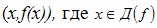 . .
|
