VI. Определенный интеграл и его приложения.
Понятие определенного интеграла.
Пусть ![]() - функция, непрерывная на интервале
- функция, непрерывная на интервале ![]() и
и ![]() - ее первообразная, то есть:
- ее первообразная, то есть: ![]()
![]() для
для ![]() .
.
Определение 1. Определенным интегралом 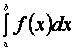 от функции
от функции ![]() на интервале
на интервале ![]() называется приращение ее первообразной:
называется приращение ее первообразной: 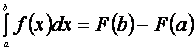 , где а – нижний предел интегрирования; b – верхний предел интегрирования;
, где а – нижний предел интегрирования; b – верхний предел интегрирования; ![]() - интервал интегрирования;
- интервал интегрирования; ![]() - подынтегральная функция; х – переменная интегрирования.
- подынтегральная функция; х – переменная интегрирования.
Таким образом, определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов интегрирования.
Обозначим ![]() , тогда
, тогда 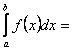
![]() .
.
Это формула Ньютона-Лейбница.
Пример: Найти интеграл от х2 в пределах от 2 до 4.
Решение. Так как ![]() - первообразная для
- первообразная для ![]() , то
, то ![]()
Замечание: Мы получим тот же результат, если используем другую первообразную для ![]() , например,
, например, ![]() или
или ![]() и т.д.
и т.д.
Теорема: определенный интеграл от непрерывной функции не зависит от выбора первообразной для подынтегральной функции.
Доказательство: Пусть ![]() и
и ![]() - две различные первообразные для функции
- две различные первообразные для функции ![]() , тогда по основному свойству первообразной имеем:
, тогда по основному свойству первообразной имеем: ![]() =
=![]() +С, где С = const, отсюда
+С, где С = const, отсюда 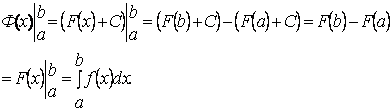
Теорема доказана.
Геометрический смысл определенного интеграла
Пусть на интервале ![]() задана непрерывная функция
задана непрерывная функция ![]()
Определение 2. Геометрическая фигура, ограниченная сверху графиком функции ![]() , снизу осью ОХ, слева и справа
, снизу осью ОХ, слева и справа ![]() и
и ![]() , называется криволинейной трапецией
, называется криволинейной трапецией
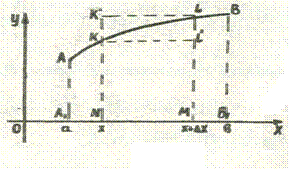
Докажем, что площадь криволинейной трапеции ![]() вычисляется по формуле
вычисляется по формуле 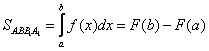 ,
,
где ![]() - первообразная для функции
- первообразная для функции ![]() на
на ![]() .
.
Рассмотрим часть криволинейной трапеции ![]() , которая находится левее точки
, которая находится левее точки ![]() . Площадь такой фигуры – это функция от х, обозначим ее
. Площадь такой фигуры – это функция от х, обозначим ее ![]() , тогда
, тогда ![]() ;
;
![]()
![]() .
.
Приращение функции ![]() в точке х
в точке х ![]() равно площади криволинейной трапеции
равно площади криволинейной трапеции ![]() :
: ![]()
![]() .
.
Для площади ![]() выполняется двойное неравенство:
выполняется двойное неравенство: ![]()
![]()
![]() .
.
Площади прямоугольников определяются формулами:
![]() ;
; ![]() , поэтому
, поэтому ![]()
![]() ;
;
или при ![]()
![]()
![]() .
.
По условию ![]() - непрерывная функция
- непрерывная функция ![]() ,
,
то есть ![]() ;
; ![]() .
.
Переходим к пределу в последнем двойном неравенстве и получаем:
![]()
![]() .
.
Следовательно, функция ![]() - первообразная для функции
- первообразная для функции ![]() :
: ![]() =
=![]() .
.
Так как ![]() ,
, ![]() =
=![]() , то
, то ![]() и
и ![]() =
=![]() .
.
Отсюда 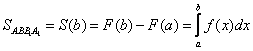 .
.
Определенный интеграл от непрерывной неотрицательной функции равен площади соответствующей криволинейной трапеции.
Основные свойства определенного интеграла
1. 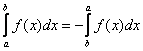
2. 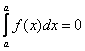
3. 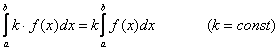
4. 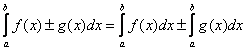
5. 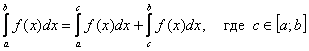
6. 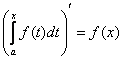
Действительно, 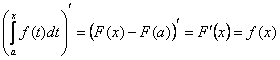 .
.
Замечание: Интеграл 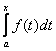 называется интегралом с переменным верхним пределом.
называется интегралом с переменным верхним пределом.
Приложение определенного интеграла
Определенный интеграл применяется для вычисления площадей плоских фигур.
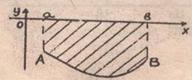
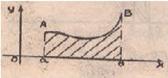
1) Пусть функция ![]() непрерывна и положительна на
непрерывна и положительна на ![]() , тогда площадь соответствующей криволинейной трапеции
, тогда площадь соответствующей криволинейной трапеции 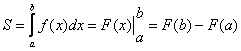 .
.
2) Пусть функция ![]() непрерывна и отрицательна на
непрерывна и отрицательна на ![]() , тогда площадь соответствующей криволинейной трапеции
, тогда площадь соответствующей криволинейной трапеции 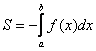 .
.
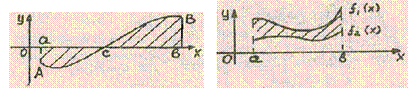 3) Пусть функция
3) Пусть функция ![]() непрерывна на
непрерывна на ![]() и принимает на этом интервале как положительные, так и отрицательные значения:
и принимает на этом интервале как положительные, так и отрицательные значения:  .
.
4) Пусть площадь фигуры ограничена двумя прямыми ![]() и
и ![]() и двумя непрерывными функциями
и двумя непрерывными функциями ![]() и
и ![]() на
на ![]() . Тогда
. Тогда 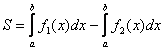 .
.
Определенный интеграл применяется для вычисления объемов тел.
Если криволинейная трапеция, ограниченная кривой ![]() и прямыми
и прямыми ![]() вращается вокруг оси ОХ, то объем тела вращения вычисляется по формуле
вращается вокруг оси ОХ, то объем тела вращения вычисляется по формуле 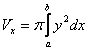 .
.

Задачи и упражнения
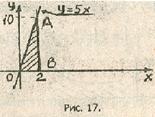
- Вычислить площадь фигуры, ограниченной линиями
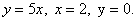
Решение:![]()
![]()
С помощью определенного интеграла 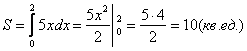
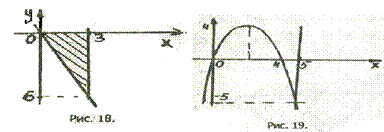 Вычислить площадь фигуры, ограниченной линиями:
Вычислить площадь фигуры, ограниченной линиями: 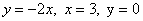 (рис.а).
(рис.а).
а) б)
Решение:
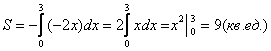
- Вычислить площадь фигуры, ограниченной линиями
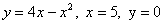 (рис.б).
(рис.б).
Решение:
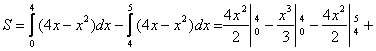
![]()
![]() .
.
- Вычислить площадь фигуры, ограниченной линиями
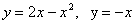 (рис.в).
(рис.в).
Построим графики функций и найдем абсциссы точек пересечения на системы: 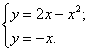
Решение:
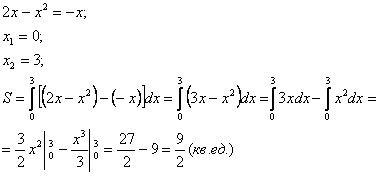
в) г)
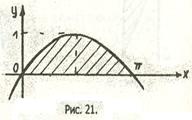
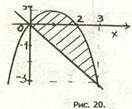
- Найти объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной
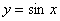 и прямыми
и прямыми 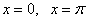 (рис.г).
(рис.г).
Решение:
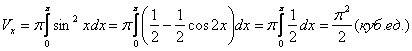
Упражнения:
- Вычислите интегралы:
1. ![]() 2.
2. 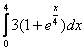 3.
3. ![]() 4.
4. ![]()
5.  , подстановка
, подстановка ![]()
6. 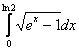 , подстановка
, подстановка ![]()
- Вычислите площади, ограниченные линиями:
а). ![]()
б). ![]()
в). ![]()
г). ![]()
- Найдите объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями:
а). ![]()
б). ![]()
