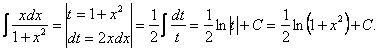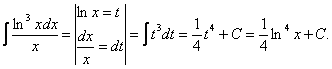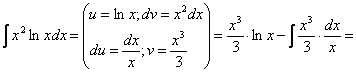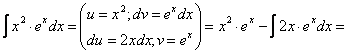V. Первообразная функция. Неопределенный интеграл.
Понятие первообразной функции.
Мы уже умеем находить для данной функции![]() ее производную
ее производную ![]() . Рассмотрим обратную задачу. По данной функции
. Рассмотрим обратную задачу. По данной функции ![]() найти такую функцию
найти такую функцию ![]() , что её производная равна
, что её производная равна ![]() , т.е
, т.е ![]() =
=![]() .
.
Определение Функция ![]() называется первообразной для функции
называется первообразной для функции![]() на интервале (а,в), если для всех х из этого интервала выполняется равенство:
на интервале (а,в), если для всех х из этого интервала выполняется равенство: ![]() =
=![]() .
.
Например:
1. Функция ![]() является первообразной для функции
является первообразной для функции![]() , т.к.
, т.к. ![]() .
.
2. Функция ![]() является первообразной для
является первообразной для ![]() , т.к.
, т.к. ![]() .
.
Теорема. Если ![]() - первообразная функция
- первообразная функция ![]() на интервале (а,в) , то функция
на интервале (а,в) , то функция ![]() , С – const, также является первообразной для
, С – const, также является первообразной для ![]() на (а;в).
на (а;в).
Доказательство: Найдем производную функции ![]() :
: ![]() .
.
Из теоремы следует, что множество функций ![]() , где
, где ![]() - одна из первообразных для функции
- одна из первообразных для функции ![]() , а С – произвольная постоянная, образует семейство первообразных для функции
, а С – произвольная постоянная, образует семейство первообразных для функции ![]() .
.
Неопределенный интеграл
Определение Множество всех первообразных функций для ![]() на интервале (а,в) называется неопределенным интегралом от функции
на интервале (а,в) называется неопределенным интегралом от функции ![]() на этом интервале и обозначается символом
на этом интервале и обозначается символом ![]() .
.
Знак ![]() - называется знаком интеграла;
- называется знаком интеграла; ![]() - подынтегральная функция;
- подынтегральная функция; ![]() - подынтегральное выражение; переменная x– переменная интегрирования.
- подынтегральное выражение; переменная x– переменная интегрирования.
Нахождение первообразной по ее производной или неопределенного интеграла по заданной подынтегральной функции называется интегрированием этой функции.
Например: 1. ![]() ; проверка
; проверка ![]()
2. ![]() ; проверка
; проверка ![]() .
.
Основные свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна подынтегральной функции:
![]() .
.
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
![]() .
.
3. Неопределенный интеграл от дифференциала некоторой функции
![]() равен
равен ![]() , то есть:
, то есть: ![]() .
.
4. Неопределенный интеграл от суммы двух или нескольких интегрируемых функций равен сумме их интегралов:
![]() .
.
5. Постоянный множитель можно вынести за знак интеграла:
![]() .
.
Основные неопределенные интегралы
2. ![]()
3.![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]()
13. ![]()
Основные методы интегрирования
1. Непосредственное интегрирования
![]()
![]() ;
;
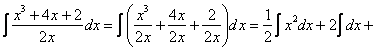
![]() ;
;
![]()
![]() .
.
2. Метод замены переменной
Теорема. Пусть функция ![]() определена на (а;в), а х – множество значений этой функции, на котором определена функция
определена на (а;в), а х – множество значений этой функции, на котором определена функция ![]() . Тогда, если функция
. Тогда, если функция ![]() имеет первообразную, на (а;в) справедлива формула:
имеет первообразную, на (а;в) справедлива формула: ![]() .
.
Например:
3. Интегрирование по частям
Некоторые интегралы можно найти с помощью формулы интегрирования по частям:
![]() , где
, где ![]() ;
; ![]() - дифференцируемые на (а;в) функции.
- дифференцируемые на (а;в) функции.
Доказательство:
1. Найдем дифференциал произведения функций ![]() и
и ![]() .
.
![]() .
.
2. Проинтегрируем это равенство:
![]() ;
;
![]() , откуда следует:
, откуда следует: ![]() .
.
Пример:
![]()
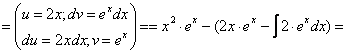
![]()
Упражнения:
Найдите интегралы:
-
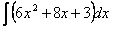 2.
2. 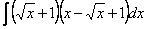
3. ![]() 4.
4. ![]()
5. ![]() 6.
6. ![]()
7. ![]() 8.
8. ![]()
9. ![]()
10. ![]() (подст-ка
(подст-ка ![]() )
)
11. Найдите функцию, производная которой ![]() , если при х=-3 эта функция принимает значение, равное 28.
, если при х=-3 эта функция принимает значение, равное 28.
12. ![]()
13. ![]()
14. ![]()
15. ![]()
16. ![]()
17. ![]()
18. ![]()
19. ![]()