Основы математического анализа

IV. Применение производных в исследовании функций.

Признак монотонности функции.

Теорема 1. Если функция  дифференцируема и  () на интервале (а;в), то она не убывает (не возрастает) на этом интервале, то есть является монотонной (не строго). Для строгой монотонности функции: при  функция возрастает, а при  функция убывает.

Точки экстремума функции

Определение. Точка х0  называется точкой максимума (минимума) функции , если для любого  в некоторой окрестности точки х0  выполняется неравенство  (). Значения функции в точке х0  называется  и .
Точки минимума и максимума объединены общим названием – «точки экстремума»
Теорема 2. (необходимое условие существования экстремума). Если функция  дифференцируема в точке х0 и имеет в этой точке экстремум, то .
Геометрический смысл теоремы 2 показан на рисунке 1. Если в точках экстремумов существуют касательные, то они параллельны оси ох.

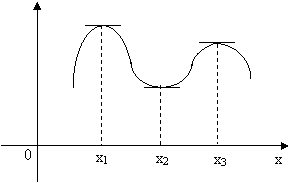
Рис.1

Точки, в которых производная равна нулю, называют точками возможного экстремума или стационарными точками.
Теорема 3 (достаточное условие существование экстремума) Пусть функция  дифференцируема в некоторой окрестности точки х0. Если при переходе через точку х0 слева направо производная  меняет знак с плюса на минус (с минуса на плюс), то в точке х0 функция имеет максимум (минимум). Если  не меняет знака в окрестности точки х0, то данная функция  не имеет экстремума в точке х0.
Например. Найти экстремум и интервалы монотонности. .
Найдем производную: .
Приравниваем ее к нулю и решаем уравнение: , . Точки 2 и 3  - точки возможного экстремума

              

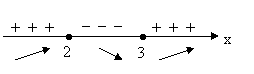
Производная  при переходе через точку  меняет знак с «+» на «-», следовательно, в этой точке максимум; при переходе через точку , производная  меняет знак с «-» на «+», следовательно, в этой точке минимум.
На интервале  и , , следовательно, функция  возрастает. На интервале  функция  убывает.

Выпуклость и точки перегиба графика функции

Определение. График функции  имеет на интервале (а,в) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (а,в) (рисунок 2).
                                                                                

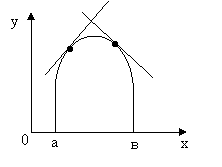
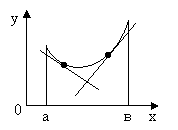
                                 Рис.2
Теорема 4  Если функция  имеет на интервале (а,в) вторую производную и  на (а,в), то график функции имеет на (а,в) выпуклость, направленную вниз (вверх).
Определение. Точка называется точкой перегиба графика функции , если в точке М график имеет касательную и существует такая окрестность точки , в пределах которой график функции  имеет разные направления выпуклости.

 

 

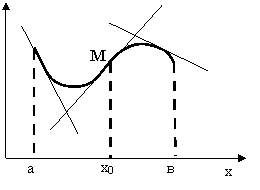
Теорема 5 (необходимое условие точки перегиба). Пусть график функции  имеет перегиб в точке , и функция  имеет в точке  непрерывную вторую производную. Тогда .
Точки графика, для которых , называются критическими. В каждой такой точке необходимо исследовать дополнительно вопрос о существовании перегиба.
Теорема 6 (достаточное условие точки перегиба). Пусть функция  имеет вторую производную в некоторой окрестности точки , которая имеет разные знаки слева и справа от . Тогда график  имеет перегиб в точке .
Например . Найдем вторую производную:  - критическая точка. Вторая производная имеет следующие знаки слева и справа от точки :

 

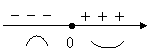
                                             (0;0) – точка перегиба.

 

Асимптоты графика функции

Если график функции неограниченно приближается к некоторой прямой, то такие прямые называют асимптотами.
Существует три вида асимптот :вертикальные, горизонтальные и наклонные.
Определение. Прямая х=а называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или  равно  или .
Определение. Прямая  называется наклонной асимптотой графика функции  при , если       (1)
Определение. Если угловой коэффициент наклонной асимптоты , то асимптота называется горизонтальной.
Если асимптоты существуют, то коэффициенты к и в  в уравнении у=кх+в находят следующим способом:
Найдем предел . Если этот предел существует, то .
Тогда находим в: в =
Если один из этих пределов не существует, то наклонных асимптот нет.
Пример. Найти асимптоты графика функции.
1) Прямая х=1 – вертикальная асимптота, так  как .

2) Найдем наклонную асимптоту, если она существует.
.
в = 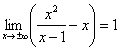, следовательно, график функции имеет наклонную асимптоту: у=х+1.

Схема исследования функции

1. Найти область определения функции.
2. Исследовать функцию на четность, нечетность, периодичность.
3. Найти точки пересечения графика функций с осями координат.
4. Найти экстремумы функции, интервалы монотонности.
5. Найти точки перегиба и интервалы выпуклости.
6. Найти асимптоты графика функции.
7. Построить график функции, используя все полученные данные.

 

Например. Построить графики функций:

1)

1. Область определения функции: .
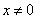2. Функция является нечетной.
3. Уравнение 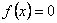 имеет корни: 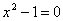,  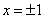(точки пересечения с осью ОХ). Пересечения с осью ОУ нет.
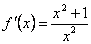4. . Производная не равна нулю, и точек экстремума нет. В области определения 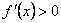, следовательно, функция возрастает на всей области своего определения.
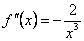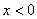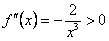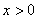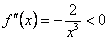5. . Если , то , и график функции выпуклый вниз. Если , то , и график функции выпуклый вверх.
6. Вертикальная асимптота – ось ОУ, так как 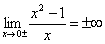. Наклонная асимптота: ;

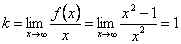в =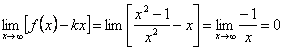
Итак, уравнение наклонной асимптоты: у=х.

 

 

1. Построим график функции:

 

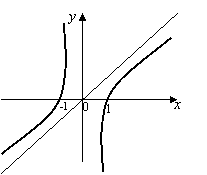
2) Дана функция
1. Область определения функции: \.
2.     - нечетная функция.
3. Нули функции: , .
4. 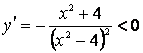 для всех х из области определения функции. Функция убывает во всей области определения функции.
5. 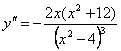. Пусть  , тогда     
Определим знаки  в области определения функции.

Функция имеет точку перегиба (0;0).

 

6.Найдем  . Отсюда следует, что
 и  - вертикальные асимптоты.
.
Отсюда следует, что  - горизонтальная асимптота.
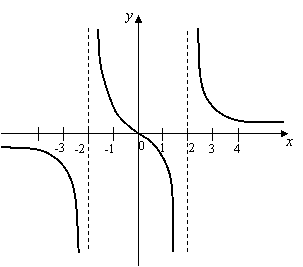
По результатам исследования функции  строим ее график: