Основы математического анализа

III. Производная.

1. Определение производной.

Пусть функция определена и непрерывна на интервале (а;в). Выберем два любых значения из этого интервала: (а;в) и (а;в).
Определение 1. Разность называется приращением аргумента функции в точке и обозначается : =
Определение 2. Приращением функции в точке называется разность между значением функции в точке и значением функции в точке :
.
Приращение функции в точке обозначают: :
.
Определение 3. Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента при , стремящемся к нулю
.
Если этот предел существует, то говорят, что функция имеет производную в точке , или что функция дифференцируема в точке .
Производную функции в точке обозначают:
; , таким образом,

.
Говорят, что функция дифференцируема в интервале (а;в), если она дифференцируема в каждой точке этого интервала.

2. Механический смысл производной

Пусть точка движется по прямой с переменной скоростью и функция описывает закон движения точки, как зависимость пути от времени . Тогда разность - это путь, пройденный за промежуток времени , а отношение - средняя скорость за время .
Если уменьшать промежуток времени так, что стремится к нулю , то определяет мгновенную скорость точки в момент времени как производную пути по времени.

3. Геометрический смысл

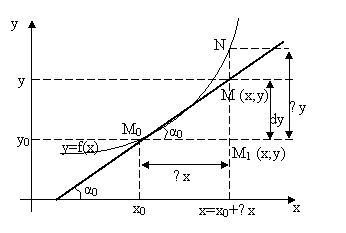
Пусть функция имеет график, который изображен на рисунке 1. Точки М и N принадлежат графику функции.
Прямая MN – секущая, она пересекает график в двух точках.
Касательной к графику функции в точке М называется предельное положение секущей MN, когда точка N стремится к точке М по кривой .
Пусть точка М на кривой соответствует значению аргумента , а точка N – значению аргумента (см.рис.1). Из определения касательной следует, что для ее существования в точке нужно, чтобы существовал предел , который равен углу наклона касательной к оси ОХ.
Из треугольника следует, что
Если производная функции в точке существует, то, согласно определению производной получаем: .
Следовательно, производная равна тангенсу угла наклона касательной к положительному направлению оси ОХ или угловому коэффициенту касательной к графику функции в точке М (,). При этом угол наклона касательной определяется из формулы: .

4. Уравнение касательной

Рис. 2
На рисунке 2 изображен график функции - точка касания прямой к графику. - любая точка на касательной. Из имеем: . Из геометрического смысла производной следует, что . Поэтому имеем: , или , или - это уравнение касательной к графику функции в точке .
Из чертежа видно, что отрезок - часть приращения функции . Эту часть приращения называют дифференциалом функции в точке и обозначают . Отношение . Можно доказать, что . Поэтому имеем: . Производную функции иногда пишут как отношение дифференциалов: .

5. Правила дифференцирования суммы, произведения и частной функции

Теорема: Если функции и дифференцируемы в точке х, то сумма (разность), произведение и частное этих функций (частное при условии ) также дифференцируемы в этой точке, причем справедливы следующие формулы:
.
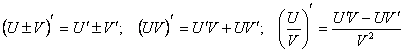Доказательство:Для вывода формул будем использовать определение производной и теоремы о пределах функций.
1.

.
Для вывода второй и третьей формул используем также равенство .
2.

.
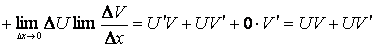Третья формула доказывается аналогично.

6. Производные некоторых элементарных функций

1. Возьмем функцию , где С – постоянное число. . .

2.

, то есть .

3. Приращение функции , откуда при получаем: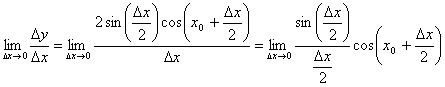 Так как: 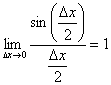(первый замечательный предел), а , то . Следовательно
Производные других элементарных функций находятся аналогично с помощью определения производной.

Таблица производных элементарных функций

1.	8.
2.	9.
3.	10.
4.	11.
5.	12.
6.	13.
7.	14.

7. Производная сложной функции

Пусть даны функции и . Функция - называется сложной функцией. Для существования сложной функции необходимо, чтобы множество значений функции входило в область определения функции .
Теорема:Если функция дифференцируема в точке х0, а функция дифференцируема в точке , то сложная функция дифференцируема в точке х0 и ее производная вычисляется по формуле: .