II. Предел последовательности и предел функции
1. Определение предела последовательности
Пусть последовательность задана общим членом: 
.
Если п неограниченно увеличивается, (стремится к бесконечности) 
, то величина 
неограниченно уменьшается (стремится к нулю) 
. Тогда выражение 
. Величина 
может стать меньше любого положительного числа, если число 
достаточно большое. Например: 
, если 
; 
, если 
;
, если 
; и т.д.
Этот пример показывает, что для данной последовательности всегда можно найти такое число N, что для всех 
, будет выполняться неравенство 
(
- (эпсилон) любое положительное число). Число 
называется пределом этой числовой последовательности.
Можно записать: 
.
Определение. Число а называется пределом последовательности 
, если для любого положительного числа 
существует такой номер N, что при всех 
выполняется неравенство: 
.
Если предел последовательности равен числу а, это записывается так: 
, или 
, при 
.
Иными словами: 
.
Если последовательность имеет предел она называется сходящейся, а если не имеет предела, расходящейся.
2. Геометрический смысл предела
Пусть дана последовательность 
с общим членом 
и эта последовательность имеет предел а, то есть 
. Из определения следует, что для всех п , больше некоторого N, выполняется неравенство: 
, или 
, 
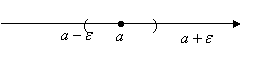
Это означает, что при 
все элементы последовательности 
находятся в 
- окрестности точки а, то есть
в интервале: (
;
).
Следовательно, если число а – предел последовательности 
, то в любой 
- окрестности точки а на числовой прямой находятся бесконечное число точек – элементов этой последовательности, тогда как вне 
- окрестности остается конечное число элементов.
3. Существование и единственность предела
Теорема 1. Если последовательность сходится, то она имеет только один предел.
Доказательство: Пусть последовательность 
имеет два различных предела: 
, 
. Тогда, по определению, будут выполняться два неравенства: 
и 
, для всех п больших некоторого натурального числа 
.
Рассмотрим 
:
.
Следовательно, числа а и в такие, что а-в меньше любого положительного числа 
. Это возможно, если а-в=0, то есть а=в. Таким образом, последовательность имеет только один предел.
Теорема 2. Если последовательность сходится, то она ограничена (без доказательства)
Замечание. Ограниченная последовательность может и не иметь предела. Например: 
; 
, ограничены, но не имеют предела. Вопрос о существовании предела сложен. Приведем только одну теорему, о достаточном условии существования предела последовательности.
Теорема 3. Если числовая последовательность монотонна и ограничена, то она имеет предел (без доказательства)
4. Теоремы о пределах
1. Предел постоянного числа равен этому числу: 
.
2. Постоянный множитель можно вынести за знак предела: 
.
3. Если существуют пределы последовательностей 
и 
, то:
а) 
;
б) 
;
в)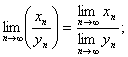 
где 
.
Теоремы о пределах доказывают с помощью определения предела последовательности.
Докажем 3а:
Пусть 
, 
, тогда по определению имеем: 
и 
.
или 
и 
.
Сложим эти неравенства: 
, или 
.
Следовательно, 
, то есть 
.
5. Бесконечно малые и бесконечно большие последовательности. Неопределенности
Определение. Сходящаяся последовательность 
называется бесконечно малой, если 
.
Определение. Последовательность 
называется бесконечно большой, если для любого положительного числа А существует такой номер N, что при 
(для всех элементов последовательности с номером 
) выполняется неравенство: 
.
В этом случае пишут: 
; 
Знак зависит от знака членов последовательности 
.
Теорема. Если 
- бесконечно большая последовательность и все ее члены не равны нулю, то последовательность 
бесконечно малая. Если все элементы бесконечно малой последовательности 
отличны от нуля, то последовательность 
бесконечно большая. (без доказательства)
Например. Последовательность 
, если 
, бесконечно большая. Тогда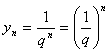 
- бесконечно малая.
При вычислении пределов последовательностей иногда встречаются неопределенности. Неопределенности бывают следующих видов:
а) Если 
и 
- две бесконечно малые последовательности, то отношение 
называется неопределенностью вида 
.
б) Если 
и 
-две бесконечно большие последовательности, то отношение 
называется неопределенностью вида 
.
в) если 
- бесконечно малая, а 
- бесконечно большая последовательности, то выражение 
называется неопределенностью вида 
.
Существуют и другие виды неопределенностей, например, 
; 
.
6. Примеры вычисления пределов последовательностей
1. В курсе математического анализа доказывается, что если 
- бесконечно малая, то 
число Непера. 
. Этот предел называют 2-ой замечательный предел.
Например:
а)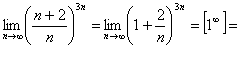 
;
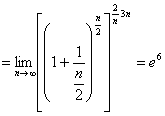б) 
.
Преобразуем данную последовательность, разделив числитель и знаменатель на 
. Применяя затем теоремы о пределе частного, предела суммы и снова о пределе частного, последовательно найдем: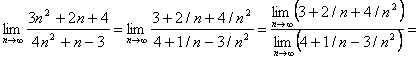 
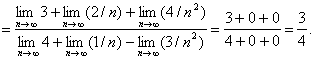
в) Найдем предел суммы п членов убывающей геометрической прогрессии, если 
.
Известно, что 
, где в1 – первый член прогрессии, 
- знаменатель прогрессии
Найдем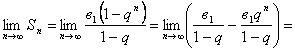 
(последовательность 
- бесконечно малая). Следовательно, 
- формула суммы членов бесконечной убывающей геометрической прогрессии.
7. Предел функции
Определение 1. Число А называется пределом функции 
в точке 
, если для любого числа 
существует такое число 
, что 
, если 
.
Пишут: 
.
Существует другое определение предела функции, эквивалентное определению 1.
Определение 2. Число А называется пределом функции 
в точке 
, если для любой последовательности 
, 
, такой что 
выполняется: 
.
Предел функции 
в точке 
существует, если выполняется критерий (условие) Коши: Если для любого числа 
существует число 
такое, что для любой пары 
и 
из области определения функции 
и удовлетворяющей условиям 
и 
выполняется неравенство: 
, то предел 
существует.
Можно доказать так же, что если предел функции существует, то он единственный. Если 
, то функция 
называется бесконечно малой в точке 
( при 
).
Если для любого числа 
выполняется неравенство 
, если 
, то функция 
называется бесконечно большой в точке 
.
Пишут: 
.
Две бесконечно малые (или бесконечно большие) в точке 
функции: 
и 
называются эквивалентными, если: 
. Пишут: 
~
, при 
Можно доказать, что при 
следующие бесконечно малые функции являются эквивалентными:
~
~
~
~
~
~
.
Для пределов функций выполняются теоремы о пределах суммы, произведения и частного функций, аналогичные подобным теоремам для последовательностей:
Теорема: Если 
; 
, то:
1. 
.
2. 
.
3. 
; 
.
8. Примеры вычисления пределов функции
При вычислении пределов функций для раскрытия неопределенностей применяют различные методы.
1) Метод преобразования функции:
Например:
2. 
.
2) Метод эквивалентных бесконечно малых:
При 
некоторые бесконечно малые функции являются эквивалентными и могут заменять друг друга.
Например, при 
: 
~ 
~ 
~ 
~ 
~ 
~ 
Найдем предел функции: 
Для вычисления других пределов применяется предел, который называется «первым замечательным пределом»: 
.
Например: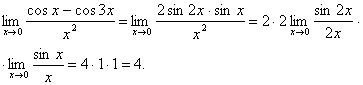 
- 1-ый замечательный предел.
Упражнения
Вычислите следующие пределы:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 