I. Числовые последовательности. Прогрессии

1. Понятие числовой последовательности

 

Рассмотрим некоторые числовые множества:
2; 4; 6; 8;…;2;… - множество четных чисел.
1; 4; 9; 16;…; ;… - множество квадратов натуральных чисел.
 - множество правильных дробей.
Между множеством натуральных чисел и этими множествами можно установить соответствия:
                
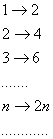
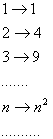
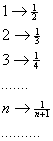
Эти соответствия являются функциями с областью определения – множеством натуральных чисел:
Определение. Функция натурального аргумента называется числовой последовательностью.
Если каждому натуральному числу n соответствует число , то говорят, что задана числовая последовательность.
Последовательность можно записать в виде:  или   ,
где  или  - первый член последовательности,
 или  - второй член последовательности,
 или  - n-й член последовательности.
Часто приходится рассматривать не всю числовую последовательность, а только ее первые n членов. Тогда говорят о конечной числовой последовательности длины n. Обозначают:
Например: множество всех двузначных чисел:

 

2. Способы задания последовательности
а) Аналитический способ задания.
Последовательность можно задать формулой общего члена. Например,
1) . Можно написать любой член этой последовательности:
2) . Получаем последовательность:
б) Рекуррентный способ задания (recurrere – возвращаться). При этом способе задания последовательности указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены.
Например,  и
; ; ;  и т.д.

3. Свойства последовательностей

а) Монотонные последовательности.
Определение. Последовательность  называется неубывающей (невозрастающей), если для всех ее членов выполняется неравенство: . В частности, последовательность  называется возрастающей (убывающей), если .
Неубывающие и невозрастающие последовательности называются монотонными, в частности, возрастающие и убывающие последовательности называются строго монотонными.
Например:  - возрастающая последовательность
 - убывающая последовательность
 - немонотонная последовательность.

 

 

б) Ограниченные и неограниченные последовательности
Определение. Последовательность  называется ограниченной сверху (снизу), если существует числа , такое, что все члены последовательности .
Например:  
Все члены последовательности меньше единицы А=1. следовательно, эта последовательность ограничена сверху.
все члены последовательности больше нуля А=0. Эта последовательность ограничена снизу.
Определение. Последовательность  называется ограниченной, если она ограничена и сверху и снизу, то есть если существует число , такое, что , для любого .
Например: ,  .
, .

Арифметическая прогрессия

Определение. Числовая последовательность называется арифметической прогрессией, если для любого натурального , начиная со второго, выполняется равенство:
,                         (1)
где , постоянное число. Число называют разностью арифметической прогрессии.
Из рекуррентной формулы (1) следует что для того чтобы задать арифметическую прогрессию, достаточно знать два числа:  - первый член прогрессии и  - ее разность. Например, если: , , то получим арифметическую прогрессию .

 

 

Формула общего члена арифметической прогрессии

По определению арифметической прогрессии можно написать:

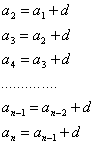
Сложим левые и правые части равенств:

                                        (2)
Формулу (2) называют формулой общего члена арифметической прогрессии.

Свойства арифметической прогрессии

1. Если  - арифметическая прогрессия, то
 ()                                             (3)
Формулу (3) называют основным свойством арифметической прогрессии.

Формула суммы п первых членов арифметической прогрессии

Обозначим сумму первых п членов арифметической прогрессии  через .
Найдем : , или .
Сложим почленно эти два равенства: , отсюда , или

5. Геометрическая прогрессия
Определение. Числовая последовательность , первый член которой , называется геометрической прогрессией, если выполняется равенство: , где называется знаменателем геометрической прогрессии.
Чтобы задать геометрическую прогрессию , достаточно задать два числа ; , где  - первый член, а  - знаменатель. Например, если ; , то получаем геометрическую прогрессию: .
Если , то все члены последовательности имеют один и тот же знак и возрастают по абсолютной величине. Например: 2; 6; 18; 54; 162;…
Если , то все члены геометрической прогрессии имеют один и тот же  знак и убывают по абсолютной величине. Например,  
Если , то все члены прогрессии возрастают по абсолютной величине и меняют знаки:  .
Если , то все члены прогрессии убывают по абсолютной величине и меняют знаки: .
Если , то все члены прогрессии одинаковы, а при  отличаются друг от друга знаком.

Свойство членов геометрической прогрессии с положительными членами

Пусть  - геометрическая прогрессия с положительными членами:;;-три ее последовательных члена, тогда :=: или
; .                            (1)
Любой член геометрической прогрессии с положительными членами, начиная со второго, равен арифметическому квадратному корню из произведения предшествующего и последующего членов.

Формула n-го члена геометрической прогрессии

Пусть дана геометрическая прогрессия  со знаменателем . Тогда по определению геометрической прогрессии:

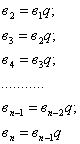
Перемножим левые и правые части равенств: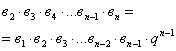
Отсюда:                                              (2)
Формула (2) – это формула общего члена геометрической прогрессии.

Формула суммы n первых членов геометрической прогрессии

Обозначим  сумму первых n членов геометрической прогрессии .
 (1). Умножим обе части на : . Но ; ; , поэтому   (2). Вычтем из равенства (2) равенство (1): ; ; , или ;  - формула суммы п первых членов геометрической прогрессии, .

Упражнения

1. Напишите первые шесть членов последовательностей, заданных формулами:
а) ;  б) ;   в)
2. Найдите формулу общего члена для следующих последовательностей:
а)     б)   
в)
3. Докажите, что последовательность с общим членом  монотонно возрастает.
4. Докажите, что последовательность с общим членом  монотонно убывает.
5.Найдите сумму первых шести членов арифметической прогрессии, если ; .
6. В арифметической прогрессии ; . Найдите сумму первых семи членов прогрессии.
7. Сумма первых пяти членов арифметической прогрессии равна 39, . Найдите .
8. Найдите пятый член геометрической прогрессии, если  и .
9. Найдите знаменатель прогрессии, если  и .
10. Найдите число п членов геометрической прогрессии, если , , .