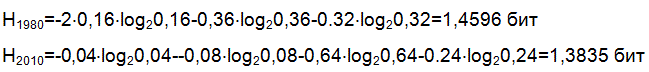2. Примеры решения задач
Решение: H = log2k = 4 бита, следовательно, k=2в4=16. Таким образом,
возможно 16 равновероятных двоичных сообщений, каждое из которых содержит
4 бита информации.
Задача 2. Дан алфавит {А1, А2, А3, А4} из которого составляют всевозможные
сообщения s длиной по три символа. Какое количество информации приходится
на одно такое сообщение?
Решение: Найдем количество возможных сообщений s: N=mn=4в3=64. Вычислим
количество информации, содержащееся в одном сообщении s, составленном из
исходного алфавита: I = log2 N= log2 64 = 6 бит.
Задача 3. Дан алфавит мощностью 4, вероятности появления букв равны
соответственно р1=р2=0,25; р3=0,34; р4 =0,16. Определить количество информации
на символ сообщения, составленного из такого алфавита.
Решение: количество информации на символ алфавита есть энтропия данного
алфавита. Так как символы алфавита неравновероятны, то энтропия равна 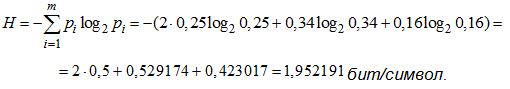
Решение. Мощность кодового алфавита т=3. В коде они комбинируются по 4,
т. е. n=4. Число сообщений такого кода N=тn=Зв4. Энтропия на одно сообщение
Н = Iog2 N = 4 Iog2 3. Количество информации в 16 сообщениях I=16?4?log23=101,44 бита.
Задача 5. Определить энтропию экрана мобильного телефона, если его разрешение
320х240, а каждый пиксель может отображать один из 4096 цветов.
Решение: предположим, что цвета пикселей равновероятны и взаимонезависимы,
тогда энтропия одного пикселя Hп=log24096=12 бит. Всего пикселей 320?240=76800,
а энтропия всего экрана Нэ=76800*12=921 600 бит.
Задача 6. Опытный индивидуальный предприниматель знает, что 25% всех его
документов составляют налоговые декларации. Для неопытного предпринимателя
появление любого типа документа – равновероятно. Определите, какое количество
информации получит опытный и неопытный предприниматели при получении налоговой декларации?
Решение: для неопытного предпринимателя появление налоговой декларации или любого документа – равновероятно, следовательно
Iнеопыт=-0.5 log20.5 - 0.5 log20.5=1 бит.
Опытный предприниматель заранее может предвидеть вероятность появления налоговой декларации, поэтому
Iопыт=-0.25 log20.25 - 0.75 log20.75=0,5+0,3113=0,8113 бит.
Задача 7. Чему равна энтропия системы, состоящей из k взаимонезависимых подсистем,
если:
1) каждая подсистема состоит из n элементов, каждый из которых с равной
вероятностью может находиться в т состояниях;
2) подсистема S1 состоит из n1
элементов, подсистема S2 состоит из n2 элементов и т.д., подсистема Sk состоит
из nk элементов, каждый из которых может с равной вероятностью находиться в
т состояниях;
3) каждая подсистема состоит из разного количества элементов,
которые с разной вероятностью могут находиться в одном из состояний? Под энтропией
системы понимается неопределенность того, что система будет находиться в о
дном из n возможных состояний.
Решение: 1) Находим энтропию одной подсистемы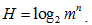
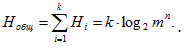
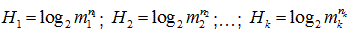
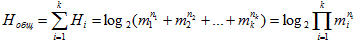
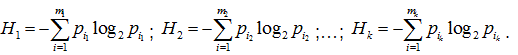
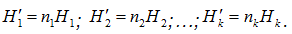
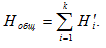
Решение: Число принятых символов, включая пробел, . Следовательно,
объем передаваемой информации 24*8=192 бита. Количество информации:
а) для равновероятного алфавита 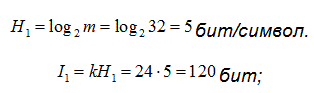
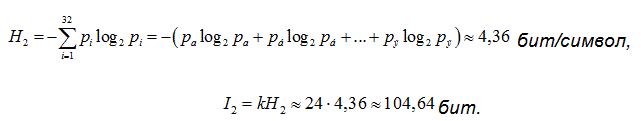
Решение: из теории известно, что чем больше энтропия некоторой группы
событий, то тем тяжелее верно угадывать наступление следующего события.
Вычислим энтропию для двух указанных случаев.