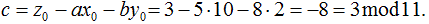3. Схема Блэкли разделения секрета
Изложим кратко (3,n)-пороговую схему Блэкли разделения
секрета. К подготовительной части этой схемы относится выбор
секретной точки 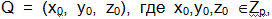 при этом y0, z0 – случайные значения, а х0 – секрет. При раздаче
секрета необходимо для каждого участника схемы выбрать случайные
значения
при этом y0, z0 – случайные значения, а х0 – секрет. При раздаче
секрета необходимо для каждого участника схемы выбрать случайные
значения 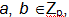 затем вычислить значение
затем вычислить значение 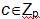 по формуле
по формуле 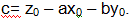
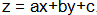
Для восстановления секрета необходимо решить систему, состоящую из
m уравнений плоскостей, которые являются легальными долями секрета.
Пример 1. Создание и восстановление секрета по (3,4)-пороговой
схеме Блэкли.
Выполним подготовительные шаги. Пусть секретом
х0 является значение 5. Выберем простое число р, превышающее
значение секрета: р=7, и еще две координаты секретной точки
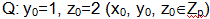 Плоскости, уравнения которых, будут выданы участникам
протокола, будут пересекаться в точке Q = (5, 1, 2).
Плоскости, уравнения которых, будут выданы участникам
протокола, будут пересекаться в точке Q = (5, 1, 2).
Вычислим доли секрета для участников протокола.
Для каждого из участников будем случайно выбирать два числа
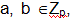 затем
вычислим значение свободного члена уравнения по формуле
затем
вычислим значение свободного члена уравнения по формуле 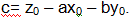
Итак, вычислим долю секрета для Алисы: а=5,
b=2, c=2-5*5-2 (mod 7)=-25 (mod 7)=-4 (mod 7)=3 (mod 7); z=5x+2y+3.
Секрет для Боба: а=-5, b=-2, c=2+5*5+2*1 (mod 7)=29 (mod 7)=1;
z=-5x-2y+1.
Секрет для Кэрол: а=2, b=-6, c=2-2*5+6*1 (mod 7)=-2
(mod 7)=5; z=2x-6y+5.
Секрет для Дейва: а=4, b=2,
c=2-4*5-2*1 (mod 7)=1; z=4x+2y+1.
Для восстановления секрета
используем доли Алисы, Боба и Дейва. Из секретов этих участников
составим систему уравнений и решим ее. Искомым секретом будет
найденное значение х. 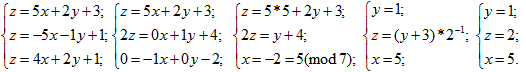
Ситуация: вы – Мэллори, сумевший втереться в доверия трех легальных
владельцев секрета (3,n)-пороговой схемы Блэкли. Участники протокола
огласили значение своих долей (Алиса: z=x-y+6, Боб: z=-6x+3y+2, Кэрол:
z=3x+4y+9, р=11), теперь вам нужно срочно вычислить «правильную» долю
секрета, чтобы вас приняли за Дейва – доверенного участника протокола.
Сначала в кольце Z11 решим систему уравнений и вычислим секрет, а
затем сгенерируем достоверную долю.