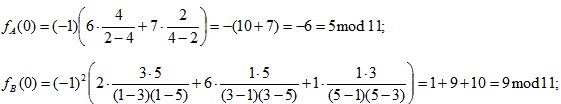|
2. Схема Шамира разделения секрета
Для создания (m,n)-пороговой схемы
Ади Шамир (Adi Shamir) предложил использовать полиномиальные
уравнения в конечном поле Fp, где p – простое число, большее
количества возможных долей n и большее любого возможного секрета
[1], [2].
К подготовительной части этой
схемы относится генерация полинома f(x) степени m-1 со случайными
коэффициентами из Fp, такого что, значение секрета равно f(0).
Долей секрета участника j (j =1,…n)
схемы является пара вида 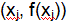 где xj=1, …, p-1. где xj=1, …, p-1.
Для восстановления секрета f(0) согласно (m,n)-
пороговой схеме Шамира используется интерполяционная формула
Лагранжа 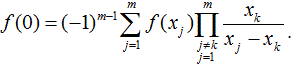
Примеры разделения и
восстановления секрета
Пример 1. Восстановления и создания секрета
по (3,n)-пороговой схеме Шамира.
Ситуация: вы – Мэллори, сумевший
втереться в доверия трех легальных владельцев секрета
(3,n)-пороговой схемы Шамира. Участники протокола огласили значение
своих долей (Алиса – (9,8), Боб – (3,8), Кэрол – (6,1), n=11),
теперь вам нужно срочно вычислить «правильную» долю секрета, чтобы
вас приняли за Дейва – доверенного участника протокола.
Вначале вычислим значение секрета,
а затем сгенерируем достоверную долю секрета.
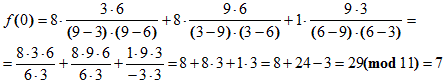
Так как рассматривается (3,n)-пороговая
схема, то очевидно, что секретные доли вычисляются с помощью
квадратного уравнения. В таком уравнении три коэффициента a, b, c.
Нам уже известно значение с=f(0)=7. Для вычисления двух оставшихся
коэффициентов составим систему из двух уравнений, используя для
этого знание долей Кэрол и Боба:
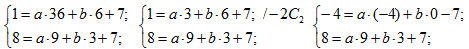
Запишем полином для вычисления долей секрета:
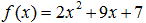 и вычислим новую «легальную»
долю секрета для х=2: и вычислим новую «легальную»
долю секрета для х=2:
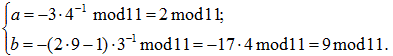
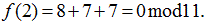 Итак, новая доля (2,0).
Итак, новая доля (2,0).
Пример 2. Разделение и восстановление
секрета между членами двух партий с использованием пороговой схемы
Шамира.
Разделим секрет N=1 между членами двух
враждующих партий А и В, таким образом, чтобы секрет можно было
восстановить только группе из не менее чем, двух членов партии А
и не менее, чем троим членам партии В. Решим эту задачу следующим
образом. Для создания долей секрета членам партии А будем
использовать линейное уравнение вида 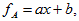
тогда для восстановления секрета нам
понадобиться 2 человека из этой партии. Для создания долей секрета
членам партии В используем квадратное уравнение вида
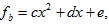
тогда для восстановления секрета нам
понадобиться 3 человека из этой партии. Итоговый результат члены
этих партий смогут получить, перемножив указанные уравнения, а
секретным значение будет являться произведение свободных членов
этих уравнений: b и e.
Создадим доли секрета. Пусть
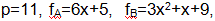 тогда 5*9 mod
11= 1. Доли секретов членов партии А: (1,0), (2,6), (3,1), (4,7),
(5,2) и так далее. Доли секретов членов партии B: (1,2), (2,1),
(3,6), (4,6), (5,1) и так далее. тогда 5*9 mod
11= 1. Доли секретов членов партии А: (1,0), (2,6), (3,1), (4,7),
(5,2) и так далее. Доли секретов членов партии B: (1,2), (2,1),
(3,6), (4,6), (5,1) и так далее.
Восстановим секрет по долям (2,6),
(4,7) участников партии А и долям (1,2), (3,6) и (5,1)
участников партии В. 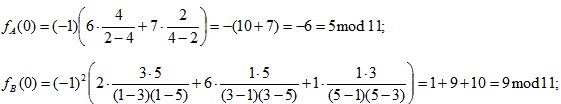
Искомый секрет N=5*9=1 mod 11.
|
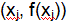 где xj=1, …, p-1.
где xj=1, …, p-1.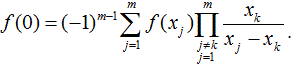
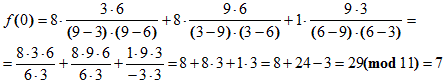
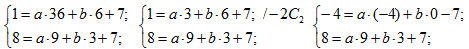
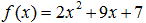 и вычислим новую «легальную»
долю секрета для х=2:
и вычислим новую «легальную»
долю секрета для х=2: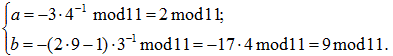
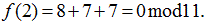 Итак, новая доля (2,0).
Итак, новая доля (2,0).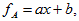
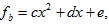
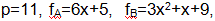 тогда 5*9 mod
11= 1. Доли секретов членов партии А: (1,0), (2,6), (3,1), (4,7),
(5,2) и так далее. Доли секретов членов партии B: (1,2), (2,1),
(3,6), (4,6), (5,1) и так далее.
тогда 5*9 mod
11= 1. Доли секретов членов партии А: (1,0), (2,6), (3,1), (4,7),
(5,2) и так далее. Доли секретов членов партии B: (1,2), (2,1),
(3,6), (4,6), (5,1) и так далее.