|
2. Алгоритм Хаффмана
Код Хаффмана – это свободный от префикса код,
который может давать самую короткую среднюю длину кода
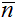 для данного входного алфавита.
Заметим, что самая короткая средняя длина кода для конкретного алфавита может
быть значительно больше энтропии алфавита источника. Алгоритм кодирования
Хаффмана может применяться для преобразования между двумя любыми алфавитами,
чаще всего его используют для преобразования произвольного алфавита в двоичный [2]. для данного входного алфавита.
Заметим, что самая короткая средняя длина кода для конкретного алфавита может
быть значительно больше энтропии алфавита источника. Алгоритм кодирования
Хаффмана может применяться для преобразования между двумя любыми алфавитами,
чаще всего его используют для преобразования произвольного алфавита в двоичный [2].
Рассмотрим работу алгоритма Хаффмана на примере.
Пример. Построить двоичный код Хаффмана
для представленного в таблице алфавита. В таблице использованы следующие
обозначения Xi – i-тый символ алфавита, Р(Xi) – вероятность появления
символа Xi.
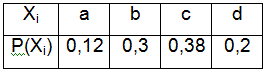
Упорядочим символы алфавита по убыванию
вероятностей их появления и сопоставим их ветвям двоичного дерева.
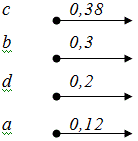
Два входа с самой низкой относительной
частотой объединим в новую ветвь. Вероятность, соответствующую этой
ветви вычислим как сумму вероятностей объединенных ветвей. После
объединения переупорядочим все ветви дерева таким образом, чтобы в
дереве сохранялась убывающая вероятность ветвей. В случае, когда
необходимо построить выходной алфавит не двоичным, а например m-ичным,
то необходимо объединять ветви дерева по m штук, которым соответствуют
наименьшие значения вероятностей.
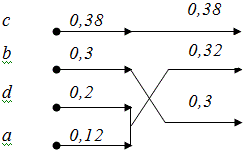
Будем продолжать этот процесс до достижения корня дерева.
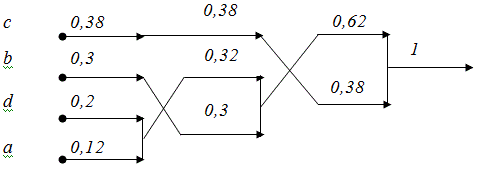
После формирования всего дерева пометим ветви,
выходящие из всех вершин символами “0” и “1”. Помечать ветви дерева можно
произвольным образом, для определенности ветвь, идущую вверх будем
помечать символом “1”, а ветвь, идущую вниз – символом “0”.
После обозначения вершин пройдем все возможные пути по дереву
от вершины (крайнее правое положение) дерева до его каждой выходной
ветви (крайнее левой положение), запоминая встретившиеся двоичные
символы. Полученные последовательности будут являться кодами символов
входного алфавита.
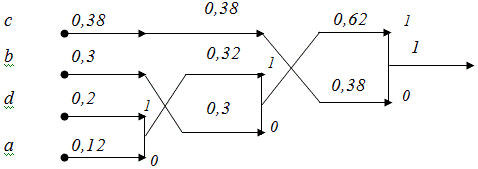
Значения, характеризующие построенный код
Хаффмана, сведем в таблицу следующего вида. В первом столбце перечислим
все символы алфавита (Xi); во втором столбце расположим
соответствующие вероятности появления символов входного алфавита Р(Xi)
; в третьем столбце запишем кодовые слова, соответствующие символам
входного алфавита; в последнем – четвертом столбце поместим значения
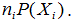
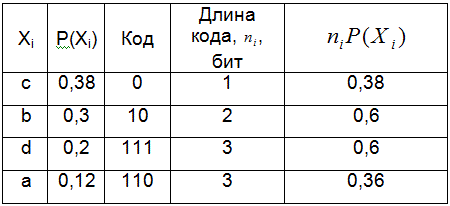
Среднюю длину кода вычислим по формуле:
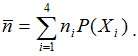
Результирующее значение
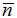 =1,94 бит
на знак, что не означает, что для передачи одного символа необходимо
передавать нецелое число бит, а означает, что для передачи 100
входных символов из алфавита мощностью 4 потребуется примерно 194
бита. =1,94 бит
на знак, что не означает, что для передачи одного символа необходимо
передавать нецелое число бит, а означает, что для передачи 100
входных символов из алфавита мощностью 4 потребуется примерно 194
бита.
|
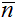 для данного входного алфавита.
Заметим, что самая короткая средняя длина кода для конкретного алфавита может
быть значительно больше энтропии алфавита источника. Алгоритм кодирования
Хаффмана может применяться для преобразования между двумя любыми алфавитами,
чаще всего его используют для преобразования произвольного алфавита в двоичный [2].
для данного входного алфавита.
Заметим, что самая короткая средняя длина кода для конкретного алфавита может
быть значительно больше энтропии алфавита источника. Алгоритм кодирования
Хаффмана может применяться для преобразования между двумя любыми алфавитами,
чаще всего его используют для преобразования произвольного алфавита в двоичный [2].




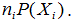

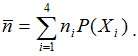
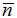 =1,94 бит
на знак, что не означает, что для передачи одного символа необходимо
передавать нецелое число бит, а означает, что для передачи 100
входных символов из алфавита мощностью 4 потребуется примерно 194
бита.
=1,94 бит
на знак, что не означает, что для передачи одного символа необходимо
передавать нецелое число бит, а означает, что для передачи 100
входных символов из алфавита мощностью 4 потребуется примерно 194
бита.